Trong thế giới toán học và hình học, khái niệm về phương trình tiếp tuyến của đường tròn đã tạo nên một sự kết nối thú vị giữa đường tròn và các đường thẳng. Không chỉ dừng lại ở lý thuyết, mà khái niệm này còn có ứng dụng rộng rãi trong nhiều lĩnh vực. Trong bài viết hôm nay, các bạn hãy cùng imo2007 khám phá sâu hơn về khái niệm quan trọng này và cách nó mang lại sự hiểu biết đa chiều về hình học và toán học nhé!
Khái niệm cơ bản về Đường Tròn và Tiếp Tuyến
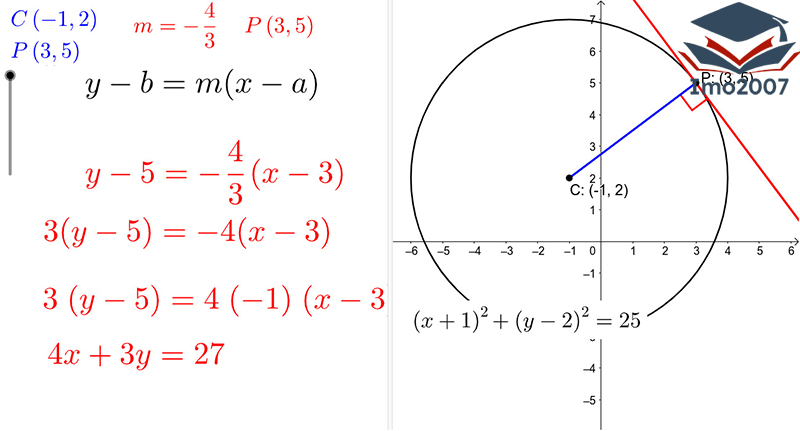
Đường tròn là một trong những khái niệm cơ bản và thú vị trong hình học, đó là tập hợp của tất cả các điểm trong mặt phẳng có khoảng cách bằng nhau tới một điểm tâm đặc biệt. Điểm tâm này chính là tâm của đường tròn và khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn được gọi là bán kính.
Nhưng khi ta tập trung vào một điểm cụ thể trên đường tròn, điều thú vị xảy ra. Tiếp tuyến tại điểm đó là một đường thẳng chỉ cắt đường tròn duy nhất tại điểm đó và không cắt nó ở bất kỳ điểm nào khác trên đường tròn. Điều này có nghĩa là tại điểm tiếp tuyến, đường thẳng này đúng như tên gọi của nó, chỉ chạm một cách duy nhất điểm trên đường tròn mà không thể cắt nó.
Để hình dung, hãy tưởng tượng một viên bi đặt trên mặt phẳng. Đường tròn chính là tập hợp các điểm trên mặt phẳng mà khoảng cách từ mỗi điểm đến tâm của viên bi là như nhau. Tiếp tuyến tại một điểm trên viên bi sẽ là đường thẳng chạm vào viên bi tại điểm đó, mà không bắt buộc phải cắt hay thấp vào viên bi ở bất kỳ vị trí nào khác.
Tìm hiểu thêm: Khám phá diện tích mặt cầu – Những điều cần biết
Công thức Phương Trình Tiếp Tuyến của Đường Tròn
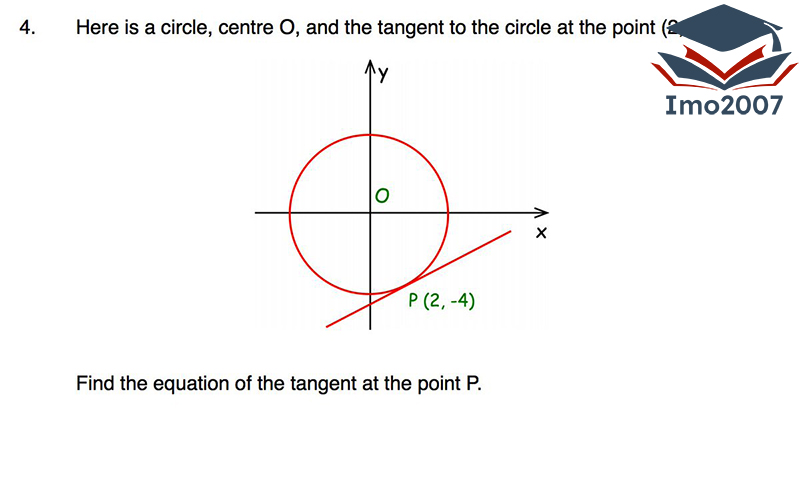
Trong phần này, chúng ta sẽ khám phá công thức phương trình tiếp tuyến của đường tròn và cách biểu diễn nó tại một điểm cụ thể trên đường tròn. Điều này giúp chúng ta hiểu rõ hơn về sự liên quan giữa hình dáng của đường tròn và tiếp tuyến tại các điểm trên nó.
Công thức chung
Phương trình tiếp tuyến của đường tròn có thể được biểu diễn bằng công thức chung sau đây:
- y−y0=m(x−x0)
Trong đó:
- m là độ dốc của đường tiếp tuyến tại điểm tiếp xúc.
- (x0 ,y0 ) là tọa độ của điểm tiếp xúc trên đường tròn.
Phương trình tiếp tuyến tại điểm có tọa độ (x0 ,y0)
Để biểu diễn phương trình tiếp tuyến của đường tròn tại một điểm cụ thể (x0,y0) trên đường tròn, chúng ta cần biết độ dốc m của đường tiếp tuyến tại điểm đó. Độ dốc m có thể được tính dựa trên độ dốc của đường tiếp tuyến tại điểm tiếp xúc trên đường tròn.
Để tính độ dốc m, chúng ta sử dụng đạo hàm của phương trình đường tròn tại điểm tiếp xúc (x0,y0). Đạo hàm này chính là độ dốc của đường tiếp tuyến tại điểm đó. Sau đó, chúng ta thay giá trị m vào công thức chung.
Ví dụ minh họa: Xét đường tròn có phương trình x2 +y2 =25, và điểm tiếp xúc là (3,4). Để tìm phương trình tiếp tuyến tại điểm này, ta thực hiện các bước sau:
- Tính đạo hàm của phương trình đường tròn theo x và y.
- Đặt x0 = 3 và y0 = 4, sau đó tính độ dốc m tại điểm tiếp xúc (3 , 4).
- Sử dụng giá trị m trong công thức chung y−y0 =m(x−x0) để có phương trình tiếp tuyến tại điểm (3 , 4).
Qua việc làm ví dụ này, chúng ta thấy rằng công thức tiếp tuyến không chỉ giúp ta xác định phương trình tiếp tuyến mà còn giúp hiểu sâu hơn về tương quan hình học giữa đường tròn và đường tiếp tuyến tại các điểm trên đường tròn.ể có phương trình tiếp tuyến cụ thể.
Xem thêm: Cách xác định góc giữa đường thẳng và mặt phẳng dễ hiểu nhất
Cách dùng phương trình tiếp tuyến để giải Toán
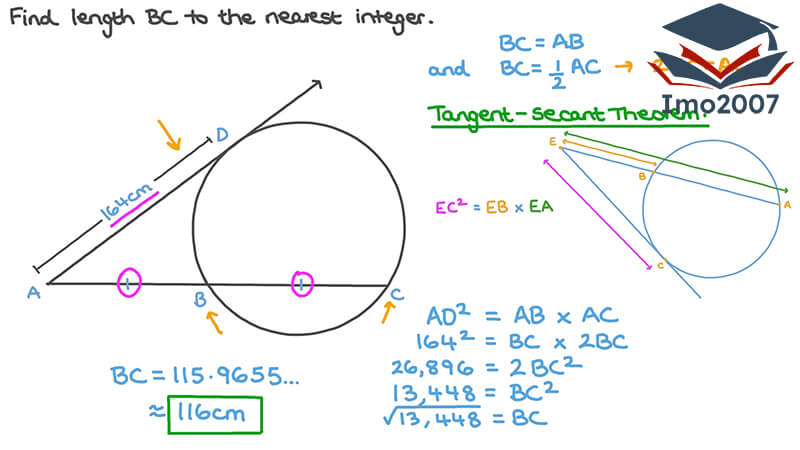
Trong phần này, chúng ta sẽ tìm hiểu cách sử dụng phương trình tiếp tuyến của đường tròn để giải quyết các bài toán thực tế và hình học. Chúng ta sẽ tập trung vào hai trường hợp cụ thể: tìm phương trình tiếp tuyến qua một điểm đã biết và tìm điểm tiếp tuyến cùng với phương trình tiếp tuyến tại điểm đó.
Tìm phương trình tiếp tuyến qua điểm đã biết
Để tìm phương trình tiếp tuyến qua một điểm tiếp xúc đã biết trên đường tròn, chúng ta cần làm các bước sau:
- Xác định tọa độ của điểm tiếp xúc (x0, y0).
- Tính độ dốc m của đường tiếp tuyến tại điểm tiếp xúc bằng cách sử dụng đạo hàm của phương trình đường tròn tại điểm đó.
- Sử dụng công thức chung y−y0=m(x−x0) với m và (x0, y0) đã biết để tìm phương trình tiếp tuyến.
Tìm điểm tiếp tuyến và phương trình tiếp tuyến tại điểm đó
Để tìm điểm tiếp tuyến và phương trình tiếp tuyến tại một điểm trên đường tròn, ta làm theo các bước sau:
- Xác định tọa độ của điểm cần tìm điểm tiếp tuyến (x,y).
- Tìm đạo hàm của phương trình đường tròn theo x và y, sau đó tính độ dốc m tại điểm cần tìm điểm tiếp tuyến.
- Sử dụng độ dốc m đã tính để giải hệ phương trình giữa x và y của đường tròn và phương trình tiếp tuyến.
- Tìm giá trị của x và y từ hệ phương trình, sau đó sử dụng giá trị này để tạo thành tọa độ của điểm tiếp tuyến.
- Sử dụng tọa độ đã tìm được để xây dựng phương trình tiếp tuyến bằng cách sử dụng công thức chung y−y0 = m(x−x0).
Qua cách thức tìm điểm tiếp tuyến và phương trình tiếp tuyến tại điểm đó, chúng ta có cơ hội áp dụng kiến thức về đạo hàm và phương trình để giải quyết các vấn đề thực tế liên quan đến đường tròn và đường tiếp tuyến.
Xem thêm: Công thức lượng giác: Khái niệm và ứng dụng cơ bản trong toán học
Ví dụ minh họa và bài toán ứng dụng
Ví dụ về tìm phương trình tiếp tuyến
Giả sử chúng ta có đường tròn có phương trình
X2 + y2 = 16 và điểm tiếp xúc là (3,−1). Chúng ta sẽ giải quyết bài toán để tìm phương trình tiếp tuyến của đường tròn tại điểm tiếp xúc này.
- Bước 1: Xác định tọa độ điểm tiếp xúc: (x0, y0)=(3,−1).
- Bước 2: Tính độ dốc m tại điểm tiếp xúc bằng cách tính đạo hàm của phương trình đường tròn theo x và y, sau đó thay vào tọa độ (3,−1) để tính m.
- Bước 3: Sử dụng công thức chung y−y0 = m(x−x0) với m và (x0, y0) để tìm phương trình tiếp tuyến.
Kết quả là phương trình tiếp tuyến tại điểm (3,−1) là y=13(x−3)−1.
Bài toán ứng dụng: Đường tròn trong thiết kế đồ họa
Trong lĩnh vực thiết kế đồ họa, phương trình tiếp tuyến của đường tròn được sử dụng để làm các hiệu ứng và đối tượng trên màn hình trở nên thực tế hơn. Ví dụ, khi ta vẽ một viên bi (được biểu thị bằng đường tròn) trên màn hình, việc tạo ra hiệu ứng “đèn sáng” hay “bóng đổ” trên bề mặt viên bi có thể được thực hiện thông qua phương trình tiếp tuyến.
Cụ thể, để tạo hiệu ứng ánh sáng và bóng đổ trên viên bi, chúng ta cần xác định vị trí của nguồn sáng (điểm) và tính toán phương trình tiếp tuyến tại điểm tiếp xúc của đường tròn đại diện cho viên bi. Điều này cho phép chúng ta xác định hướng ánh sáng và vùng bị che phủ bởi bóng đổ.
Việc áp dụng phương trình tiếp tuyến trong thiết kế đồ họa cho phép chúng ta tạo ra những hình ảnh sống động và chân thực hơn trên màn hình, tận dụng sự tương quan hình học giữa đường tròn và tiếp tuyến tại các điểm trên nó.
Xem thêm: Mẹo học công thức hạ bậc hay nhất
Phương trình tiếp tuyến của đường tròn không chỉ là một khái niệm hình học mà còn là một công cụ quan trọng trong việc giải quyết bài toán và ứng dụng thực tế. Việc hiểu và áp dụng khái niệm này sẽ giúp chúng ta nắm vững hơn về tương tác giữa hình học và toán học trong thế giới xung quanh chúng ta. Hãy đón đọc thêm những bài viết tiếp theo của imo2007 để có thêm nhiều kiến thức toán học hữu ích nhé!