Công thức lượng giác (Công thức góc) là một khái niệm quan trọng và cơ bản trong toán học, đóng vai trò quan trọng trong việc phân tích hàm số và giải các bài toán liên quan đến tam giác. Nhờ vào công thức này, chúng ta có thể tính toán các giá trị của các hàm số lượng giác và áp dụng trong nhiều lĩnh vực, từ hình học, tính toán, vật lý đến kỹ thuật. Trong bài viết này, các bạn hãy cùng imo2007eduvn khám phá sâu hơn về các công thức góc cơ bản và ứng dụng của chúng trong thực tế nhé.
Giới thiệu về Công thức lượng giác
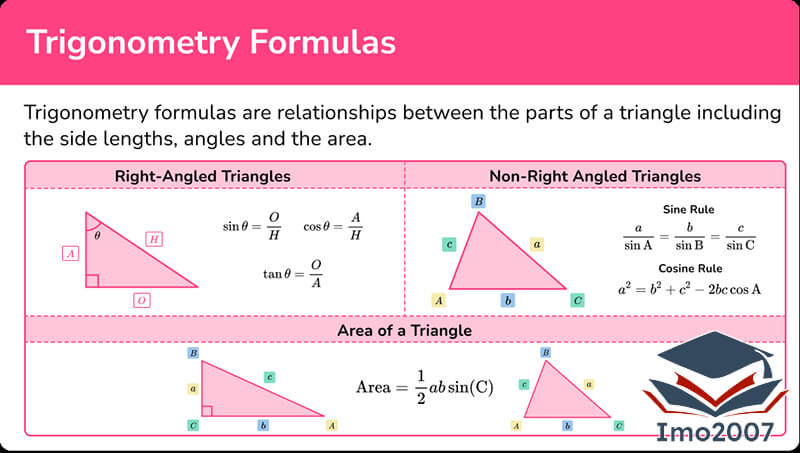
Công thức lượng giác là một tập hợp các quy tắc và mối quan hệ giữa các góc và các cạnh trong tam giác. Được định nghĩa dựa trên các hàm số lượng giác như sin, cos, tan và các hàm số nghịch đảo của chúng, Công thức góc giúp chúng ta xác định và tính toán các giá trị của các góc và cạnh trong tam giác vuông và các tam giác không vuông.
Từ việc nắm vững công thức góc, chúng ta có thể xác định các đại lượng quan trọng trong tam giác như độ dài các cạnh, độ dài các đoạn thẳng vuông góc, và đoạn thẳng đối diện với các góc trong tam giác. Công thức góc cũng có vai trò quan trọng trong việc giải các bài toán liên quan đến tam giác, từ tính toán góc, cạnh, đến ứng dụng trong hình học và vật lý.
Vì vậy, việc nắm vững Công thức lượng giác là một kỹ năng quan trọng trong phân tích hàm số và giải các bài toán liên quan đến tam giác. Trong phạm vi toán học và các lĩnh vực liên quan, Công thức góc luôn được coi là nền tảng cơ bản để hiểu và ứng dụng các khái niệm và công thức phức tạp hơn.
Xem thêm: Mẹo học công thức hạ bậc hay nhất
Các công thức lượng giác cơ bản
Công thức sin, cos, tan, csc, sec, cot trong tam giác vuông
Trong tam giác vuông, các Công thức góc cơ bản là các quy tắc xác định tỷ lệ giữa các cạnh của tam giác và các góc tương ứng. Các công thức góc cơ bản bao gồm:
- Sin: sinθ = đối diện / cạnh huyền
- Cos: cosθ = góc kề / cạnh huyền
- Tan: tanθ = đối diện / góc kề
- Csc: cscθ = 1 / sinθ
- Sec: secθ = 1 / cosθ
- Cot: cotθ = 1 / tanθ
Các công thức này cho phép chúng ta tính toán các giá trị của các hàm số lượng giác và xác định các đại lượng quan trọng trong tam giác vuông, như độ dài các cạnh, góc và tỉ lệ giữa chúng.
Công thức biến đổi lượng giác và ứng dụng trong các bài toán
Ngoài các Công thức cơ bản, chúng ta cũng có các Công thức biến đổi lượng giác như tích góc, đảo góc, công thức lượng giác bán kính, và nhiều quy tắc biến đổi khác. Nhờ vào những công thức này, chúng ta có thể đưa ra các phương pháp tính toán linh hoạt và chính xác hơn trong giải các bài toán phức tạp liên quan đến tam giác.
Ứng dụng của Công thức biến đổi lượng giác xuất hiện trong nhiều lĩnh vực, từ hình học, vật lý, thiết kế đồ họa đến các ngành kỹ thuật và khoa học xã hội. Việc hiểu và ứng dụng các Công thức biến đổi lượng giác sẽ giúp chúng ta giải quyết các bài toán phức tạp một cách hiệu quả và chính xác hơn.
Xem thêm: Công thức tính diện tích hình thang tổng hợp và đầy đủ nhất
Ứng dụng của Công thức lượng giác trong tính toán và hình học
Công thức lượng giác không chỉ có tầm quan trọng trong tính toán giá trị của các hàm số lượng giác mà còn có ứng dụng rộng rãi trong tính toán và hình học. Dưới đây là hai ví dụ về ứng dụng của Công thức góc trong các lĩnh vực này:
Sử dụng Công thức lượng giác để tính các giá trị của các hàm số lượng giác
Các công thức góc như sin, cos, tan, csc, sec, cot cho phép chúng ta tính toán các giá trị của các hàm số lượng giác dựa trên các góc trong tam giác. Chúng ta có thể áp dụng các công thức này trong việc giải các bài toán liên quan đến tam giác vuông và các tam giác không vuông. Việc tính toán các giá trị lượng giác rất hữu ích trong các bài toán vật lý, kỹ thuật, và các lĩnh vực khoa học khác.
Ứng dụng trong tính toán góc và khoảng cách trong hình học
Công thức góc cũng đóng vai trò quan trọng trong tính toán góc và khoảng cách trong hình học. Nhờ vào các Công thức góc, chúng ta có thể tính toán góc giữa các đoạn thẳng, góc giữa các đoạn thẳng và mặt phẳng, hay tính toán khoảng cách giữa các điểm trong không gian. Điều này làm cho Công thức góc trở thành một công cụ quan trọng trong việc giải quyết các bài toán hình học phức tạp và ứng dụng trong xây dựng, thiết kế, và các lĩnh vực khác.
Như vậy, việc hiểu và ứng dụng Công thức góc trong tính toán và hình học đóng góp không nhỏ vào sự phát triển và ứng dụng của toán học trong thực tế. Chúng ta có thể áp dụng các Công thức góc để giải quyết nhiều bài toán thực tế một cách chính xác và hiệu quả.
Công thức lượng giác trong các phương trình và bất đẳng thức
Công thức góc không chỉ hữu ích trong tính toán giá trị các hàm số lượng giác mà còn đóng vai trò quan trọng trong giải các phương trình và bất đẳng thức lượng giác. Dưới đây là hai ví dụ về ứng dụng của Công thức góc trong các lĩnh vực này:
Sử dụng Công thức lượng giác để giải các phương trình lượng giác
Các phương trình lượng giác là các phương trình mà biến số xuất hiện dưới dạng hàm số lượng giác, ví dụ như sin(x) = 0, cos(x) = 1/2, tan(x) = 2, vv. Để giải các phương trình này, chúng ta có thể sử dụng Công thức góc để tìm các giá trị của góc x thỏa mãn phương trình. Việc giải phương trình lượng giác đòi hỏi khả năng áp dụng Công thức lượng giác một cách linh hoạt và chính xác để tìm nghiệm của phương trình.
Áp dụng trong việc giải bất đẳng thức lượng giác
Các bất đẳng thức lượng giác là các bất đẳng thức mà biến số xuất hiện dưới dạng hàm số lượng giác, ví dụ như sin(x) < 0, cos(x) > 1/2, tan(x) ≥ 2, vv. Chúng ta có thể sử dụng Công thức góc để xác định khoảng giá trị của biến số thỏa mãn bất đẳng thức. Việc giải bất đẳng thức lượng giác giúp chúng ta tìm các khoảng giá trị của biến số mà bất đẳng thức đúng, từ đó giải quyết các bài toán liên quan đến giới hạn và tối ưu.
Như vậy, việc sử dụng Công thức góc để giải các phương trình và bất đẳng thức lượng giác đóng góp vào việc giải quyết các bài toán phức tạp và hiểu rõ hơn về các tính chất của các hàm số lượng giác. Kỹ năng này rất hữu ích trong nhiều lĩnh vực toán học và các ngành khoa học ứng dụng.
Công thức lượng giác trong vật lý và kỹ thuật
Công thức lượng giác không chỉ hữu ích trong toán học mà còn có ứng dụng rộng rãi trong vật lý và kỹ thuật. Dưới đây là mô tả về ứng dụng của Công thức góc trong tính toán và mô hình hóa các hiện tượng trong vật lý và kỹ thuật:
Ứng dụng của Công thức lượng giác trong tính toán và các hiện tượng trong vật lý
Trong vật lý, Công thức góc được sử dụng để mô tả và tính toán các hiện tượng có liên quan đến góc, tốc độ, gia tốc và các đại lượng khác. Ví dụ, trong cơ học, khi mô hình hóa chuyển động của các vật thể, Công thức góc giúp tính toán tốc độ và gia tốc của chúng dựa trên các thông số góc và thời gian. Trong điện từ, Công thức lượng giác giúp tính toán các thông số của sóng điện từ và hiệu ứng từ.
Ví dụ về ứng dụng của Công thức lượng giác trong các bài toán thực tế
- Ứng dụng trong đo lường và định vị: Trong các hệ thống đo lường và định vị, Công thức góc được sử dụng để tính toán khoảng cách và góc giữa các vật thể. Ví dụ, trong điện tử, Công thức góc giúp tính toán khoảng cách từ một thiết bị đo đến một vật thể dựa trên góc nhìn và tín hiệu nhận được.
- Ứng dụng trong xây dựng: Trong xây dựng, Công thức góc được sử dụng để tính toán chiều cao, khoảng cách, và góc của các cấu trúc và công trình. Ví dụ, trong thiết kế kiến trúc, Công thức góc giúp tính toán góc nghiêng của mái nhà, độ cao của tòa nhà và các thông số khác của công trình.
- Ứng dụng trong công nghệ: Trong công nghệ, Công thức góc được sử dụng để mô hình hóa và tính toán các hiện tượng liên quan đến sóng, tín hiệu, và các đại lượng khác. Ví dụ, trong viễn thông, Công thức góc giúp tính toán góc hướng của anten và khoảng cách truyền thông.
Như vậy, Công thức góc đóng góp vào việc mô hình hóa và tính toán các hiện tượng trong vật lý và kỹ thuật, từ đó ứng dụng vào nhiều lĩnh vực thực tế để giải quyết các bài toán phức tạp và cải thiện hiệu suất của các hệ thống.
Bài tập thực hành

Dưới đây là 5 bài tập thực hành kèm theo đáp án để các bạn có thể luyện tập thêm về công thức này:
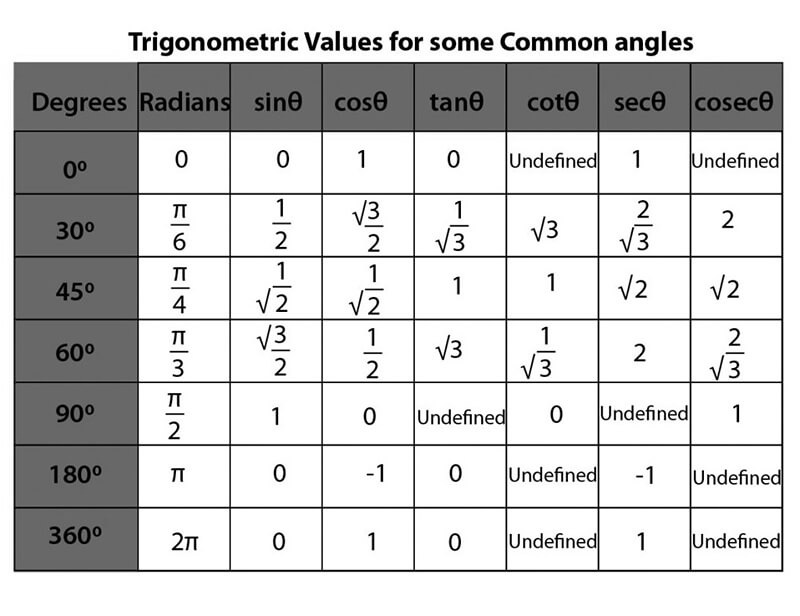
Bài tập 1: Tính giá trị của các hàm số lượng giác Tính giá trị của sin(30°), cos(45°), tan(60°), csc(45°), sec(30°), và cot(60°).
Đáp án:
- sin(30°) = 0.5
- cos(45°) = 0.707
- tan(60°) = 1.732
- csc(45°) = 1.414
- sec(30°) = 2.0
- cot(60°) = 0.577
Bài tập 2: Tính toán góc trong tam giác vuông
Cho tam giác vuông ABC với AB = 5 và AC = 3. Tính giá trị của sin(A), cos(A), và tan(A).
Đáp án:
- sin(A) = 3/5
- cos(A) = 4/5
- tan(A) = ¾
Bài tập 3: Giải phương trình lượng giác
Giải phương trình sau: tan(x) = 1
Đáp án: Để giải phương trình, ta cần tìm các giá trị của x thỏa mãn tan(x) = 1. Các góc đối ứng với giá trị tan(x) = 1 là x = π/4 + kπ, với k là số nguyên.
Bài tập 4: Giải bất đẳng thức lượng giác
Giải bất đẳng thức sau: sin(x) < 0
Đáp án: Bất đẳng thức sin(x) < 0 xảy ra khi và chỉ khi các góc x nằm trong khoảng (π, 2π).
Bài tập 5: Áp dụng Công thức góc trong bài toán thực tế
Cho cây cột cao 10 mét đứng thẳng đứng trên mặt đất. Tìm khoảng cách từ chân cây đến điểm A trên cây sao cho góc nhìn từ điểm A đến đỉnh cây là 30°.
Đáp án: Để tính khoảng cách từ chân cây đến điểm A, ta có tan(30°) = chiều cao của cây / khoảng cách cần tìm. Khi đó, khoảng cách cần tìm sẽ là 10 / tan(30°) = 10 / 0.577 = 17.32 mét (làm tròn đến 2 chữ số thập phân).
Xem thêm: Đạo hàm và vai trò quan trọng trong toán học: Khám phá sức mạnh của tính toán biến đổi
Qua bài viết này, chúng ta đã tìm hiểu về khái niệm và tầm quan trọng của Công thức lượng giác trong phân tích hàm số và giải các bài toán liên quan đến tam giác. Chúng ta đã khám phá các Công thức góc cơ bản và cách sử dụng chúng để tính toán các giá trị lượng giác và xác định các đại lượng trong tam giác. Hẹn gặp lại các bạn trong các bài viết tiếp theo của imo2007eduvn nhé!