Bạn có từng tự hỏi về mặt cầu và cách tính diện tích của nó? Trong bài viết này, chúng ta sẽ cùng khám phá về diện tích mặt cầu – một khái niệm không chỉ thú vị mà còn rất hữu ích trong học tập và cuộc sống hàng ngày. Hãy cùng imo2007eduvn dành chút thời gian để tìm hiểu về chủ đề này nhé!
Giới thiệu chung về mặt cầu

Mặt cầu là một hình học đặc biệt, được hình thành bởi việc quay một đường tròn quanh trục của nó. Khi đó, mỗi điểm trên bề mặt của hình tròn này sẽ cách đều tâm của nó một khoảng cố định, tạo thành một hình cầu đồng tâm đẹp mắt. Trong không gian ba chiều, mặt cầu là một trong những hình dạng phổ biến và quen thuộc.
Tầm quan trọng của diện tích mặt cầu trong học tập
Diện tích của mặt cầu là một khái niệm toán học quan trọng và có ứng dụng rộng rãi trong nhiều lĩnh vực. Trong chương trình học, kiến thức về diện tích mặt cầu là một phần không thể thiếu của học sinh trong môn hình học và toán học hình học không gian. Hiểu biết về diện tích của mặt cầu giúp các bạn xây dựng nền tảng kiến thức vững chắc về hình học và chuẩn bị cho những kiến thức cao hơn trong tương lai.
Ngoài ra, khái niệm diện tích của mặt cầu cũng có những ứng dụng thực tế quan trọng, đặc biệt trong các ngành kỹ thuật, xây dựng, kiến trúc và công nghệ. Việc tính toán diện tích của mặt cầu là một kỹ năng quan trọng trong việc thiết kế và xây dựng các đối tượng tròn và hình cầu như bể chứa, đường ống, bóng đèn, vòng bi, và nhiều ứng dụng khác.
Chúng ta hãy cùng tìm hiểu công thức tính diện tích của mặt cầu và những ứng dụng thú vị của nó, để có thêm kiến thức hữu ích và ứng dụng rộng rãi trong cuộc sống và công việc hàng ngày.
Xem thêm: Tính góc giữa hai đường thẳng: Khái niệm và phương pháp tính toán
Công thức tính diện tích mặt cầu
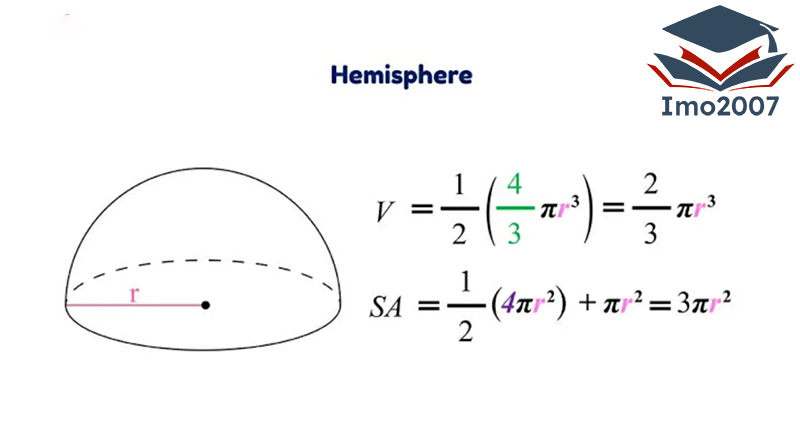
Công thức diện tích của mặt cầu là gì?
Diện tích mặt cầu là diện tích của bề mặt bên ngoài của một hình cầu. Đối với mặt cầu, diện tích không được tính theo chiều dài và chiều rộng như các hình bình thường, mà được tính trực tiếp trên bề mặt cong của hình cầu. Đây là một trong những khái niệm quan trọng trong hình học không gian và có ứng dụng rộng trong nhiều lĩnh vực.
Giải thích ý nghĩa từng thành phần trong công thức
Công thức tính diện tích mặt cầu là: A = 4πr^2
Trong đó:
- A là diện tích của mặt cầu.
- π (pi) là một hằng số xấp xỉ bằng 3.14 hoặc có thể sử dụng giá trị chính xác hơn là 3.14159.
- r là bán kính của mặt cầu, đây là khoảng cách từ tâm của mặt cầu tới bất kỳ điểm nào trên bề mặt của nó.
Ví dụ minh họa về cách tính diện tích của mặt cầu
Giả sử chúng ta có một hình cầu với bán kính r = 5 cm. Bây giờ, để tính diện tích mặt cầu, ta sẽ sử dụng công thức A = 4πr^2.
Thay vào giá trị bán kính r = 5 cm vào công thức:
- A = 4π(5 cm)^2 = 4π(25 cm^2) = 100π cm^2
Vậy diện tích của mặt cầu của hình cầu này là 100π cm^2 hoặc khoảng 314.16 cm^2 (nếu lấy π là 3.14159).
Đây chính là diện tích của bề mặt bên ngoài của hình cầu với bán kính 5 cm. Việc tính toán diện tích của mặt cầu giúp chúng ta hiểu rõ hơn về hình dạng của mặt cầu và ứng dụng rộng rãi trong thực tế như tính diện tích các bề mặt tròn, thiết kế các hình cầu trong kỹ thuật và nhiều ứng dụng khác.
Xem thêm: Công thức lượng giác: Khái niệm và ứng dụng cơ bản trong toán học
Ứng dụng diện tích của mặt cầu trong thực tế
Các ví dụ về việc tính diện tích của mặt cầu trong đời sống hàng ngày
- Bóng chày và bóng đá: Diện tích của mặt cầu của bóng chày và bóng đá là một ví dụ phổ biến trong thể thao. Các nhà sản xuất cần tính toán diện tích bề mặt của bóng để thiết kế và chọn chất liệu phù hợp, đảm bảo bóng có đặc tính chạy, bay và quả bóng đều đặn.
- Hộp số và đĩa phanh trong ô tô: Một số bộ phận trong ô tô, như hộp số và đĩa phanh, có hình dạng gần như mặt cầu. Việc tính diện tích mặt cầu giúp kỹ sư thiết kế các bộ phận này sao cho hiệu quả và bền bỉ.
- Thiết kế hộp quà: Nhiều hộp quà có hình dạng lồi, giống như một nửa mặt cầu. Việc tính diện tích của mặt cầu giúp tính toán lượng giấy, vải hoặc chất liệu trang trí cần thiết để bọc bên ngoài hộp quà.
Ứng dụng diện tích mặt cầu trong ngành công nghiệp
- Tính dung tích bồn chứa và bể chứa: Trong ngành công nghiệp hóa chất và xây dựng, việc tính toán diện tích của mặt cầu giúp xác định dung tích của bồn chứa, bể chứa chất lỏng, khí hoặc bột.
- Tính diện tích vòng bi: Trong ngành công nghiệp cơ khí, diện tích của mặt cầu được sử dụng để tính toán diện tích bề mặt của vòng bi, giúp đánh giá độ bền và chất lượng của vòng bi.
- Tính diện tích ống dẫn dầu và khí: Trong ngành dầu khí và năng lượng, diện tích của mặt cầu được sử dụng để tính toán diện tích bề mặt của ống dẫn dầu và khí, giúp ước lượng lượng dầu và khí có thể dẫn qua ống.
- Thiết kế đèn chiếu sáng và gương cầu: Trong ngành điện tử và chiếu sáng, diện tích của mặt cầu được sử dụng để thiết kế các đèn chiếu sáng và gương cầu, đảm bảo hiệu suất và chất lượng ánh sáng tốt nhất.
Tóm lại, diện tích mặt cầu có ứng dụng rộng rãi trong nhiều lĩnh vực, từ đời sống hàng ngày đến các ngành công nghiệp. Hiểu biết về diện tích của mặt cầu giúp chúng ta ứng dụng kiến thức toán học vào thực tế một cách hiệu quả và hữu ích.
Luyện tập
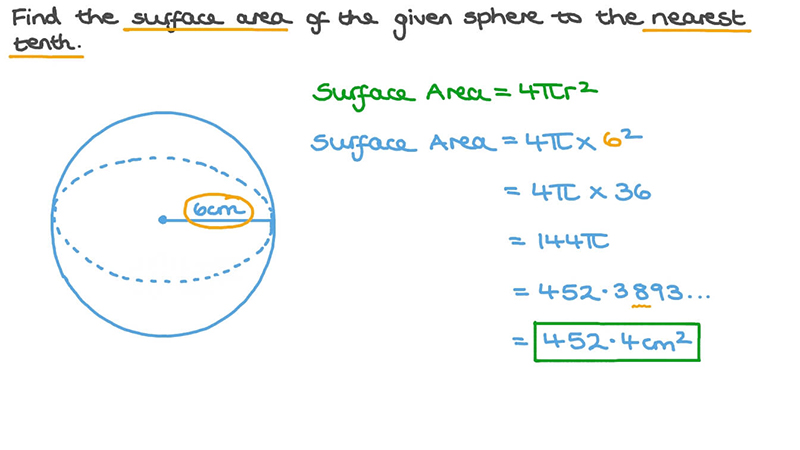
Bài toán thực hành: Tính diện tích của mặt cầu với các giá trị đề cho
- Bài toán 1: Cho một hình cầu có bán kính r = 8 cm. Hãy tính diện tích mặt cầu của hình cầu này.
- Bài toán 2: Bạn đang thiết kế một chiếc hộp quà hình cầu cho người thân. Bán kính của hộp quà là 10 cm. Tính diện tích bề mặt bên ngoài của chiếc hộp quà.
- Bài toán 3: Trong nhà bạn có một hộp chứa nước hình cầu với bán kính là 15 cm. Hãy tính diện tích của mặt cầu của hộp chứa nước này.
Hướng dẫn giải bài tập và thực hiện tính toán
Để giải các bài toán tính diện tích mặt cầu, ta sử dụng công thức A = 4πr^2, trong đó A là diện tích mặt cầu và r là bán kính của mặt cầu.
Bài toán 1:
Bán kính của hình cầu r = 8 cm.
Tính diện tích mặt cầu bằng cách thay giá trị r vào công thức:
- A = 4π(8 cm)^2
- A = 4π(64 cm^2)
- A = 256π cm^2
Kết quả là diện tích mặt cầu là 256π cm^2 hoặc khoảng 803.84 cm^2 (nếu lấy π là 3.14159).
Bài toán 2:
Bán kính của hộp quà r = 10 cm.
Tính diện tích bề mặt bên ngoài của hộp quà bằng cách sử dụng công thức:
- A = 4π(10 cm)^2
- A = 4π(100 cm^2)
- A = 400π cm^2
Kết quả là diện tích bề mặt bên ngoài của hộp quà là 400π cm^2 hoặc khoảng 1256.64 cm^2 (nếu lấy π là 3.14159).
Bài toán 3:
Bán kính của hộp chứa nước r = 15 cm.
Tính diện tích của mặt cầu của hộp chứa nước bằng cách sử dụng công thức:
- A = 4π(15 cm)^2
- A = 4π(225 cm^2)
- A = 900π cm^2
Kết quả là diện tích mặt cầu của hộp chứa nước là 900π cm^2 hoặc khoảng 2827.43 cm^2 (nếu lấy π là 3.14159).
Nhắc nhở:
- Khi tính toán, làm tròn đáp án đến hai chữ số thập phân (nếu cần thiết) để kết quả dễ đọc và hiểu quả hơn.
- Để làm quen với công thức và tính toán diện tích của mặt cầu, hãy thực hiện thêm nhiều bài tập luyện tập khác với các giá trị bán kính khác nhau.
Xem thêm: Công thức tính diện tích tam giác: Bước vào thế giới hình học
Trong bài viết này, chúng ta đã cùng nhau khám phá về diện tích của mặt cầu và tầm quan trọng của nó trong học tập và cuộc sống hàng ngày. Việc tính toán diện tích mặt cầu không chỉ là một kiến thức cơ bản trong hình học, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực, từ công nghiệp đến thiết kế đồ vật trong cuộc sống. Hẹn gặp lại các bạn trong các bài viết tiếp theo của imo2007eduvn nhé!