Diện tích tam giác là một khái niệm quan trọng trong toán học và hình học. Nó giúp chúng ta xác định diện tích bề mặt của hình tam giác, đóng vai trò quan trọng trong giáo dục và cả thực tiễn. Trong bài viết này, chúng ta sẽ tìm hiểu các công thức tính diện tích tam giác cơ bản, cách tính bằng công thức Heron và thông qua định lý cosin và sin, cũng như ứng dụng của nó trong thực tế. Hãy cùng imo2007 khám phá sự hấp dẫn của diện tích tam giác và cách áp dụng nó vào các bài toán thực tế nhé!
Giới thiệu về diện tích hình tam giác

Khái niệm và ý nghĩa của diện tích tam giác trong toán học và hình học
Diện tích tam giác là một khái niệm cơ bản trong toán học và hình học, đo lường khu vực bị bao phủ bởi ba cạnh của tam giác. Diện tích tam giác được tính bằng đơn vị đo diện tích như đơn vị bình phương, đơn vị mét vuông, và có thể biểu diễn các khu vực hình học thực tế như mặt đất, mặt biển, hay diện tích các đa giác phức tạp hơn.
Khái niệm diện tích tam giác có ảnh hưởng quan trọng đến nhiều lĩnh vực trong toán học, từ hình học đại số, hình học Euclide, đến hình học không gian ba chiều và hình học nâng cao. Nó cũng có sự liên kết mật thiết với các khái niệm khác như chu vi, đối xứng, tọa độ, và tỷ lệ trong hình học.
Tầm quan trọng của tính diện tích tam giác trong giáo dục và thực tiễn
Tính diện tích tam giác không chỉ giúp chúng ta hiểu rõ các khái niệm cơ bản của hình học mà còn có tầm quan trọng đáng kể trong giáo dục và thực tiễn. Dưới đây là một số điểm quan trọng:
- Ứng dụng hình học: Diện tích tam giác là một trong những khái niệm cơ bản của hình học và được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau như kiến trúc, xây dựng, thiết kế, định vị, đo lường và trong nghiên cứu các hiện tượng tự nhiên.
- Xây dựng kiến thức hình học: Tính diện tích tam giác giúp học sinh xây dựng kiến thức về hình học và là cơ sở để giải quyết các bài toán phức tạp hơn, từ tính diện tích các hình đơn giản đến tính toán diện tích các hình dạng phức tạp.
- Phát triển tư duy logic: Tính diện tích tam giác đòi hỏi học sinh phải áp dụng kiến thức và tư duy logic để giải quyết các bài toán. Việc này giúp phát triển khả năng tư duy, suy luận và cải thiện kỹ năng giải quyết vấn đề.
- Ứng dụng trong thực tế: Tính diện tích tam giác là một kỹ năng thiết yếu trong nhiều tình huống thực tế, từ xây dựng công trình đến định vị vị trí, tính toán lãi suất trong tài chính hay dự báo diện tích đất trong kinh doanh bất động sản.
Với tầm quan trọng đa dạng và ứng dụng rộng rãi, hiểu và áp dụng tính diện tích tam giác là một kỹ năng quan trọng giúp chúng ta giải quyết các bài toán hình học và các vấn đề thực tế hiệu quả.
Xem thêm: Công thức lượng giác: Khái niệm và ứng dụng cơ bản trong toán học
Các công thức tính diện tích hình tam giác

Diện tích tam giác vuông
Trong tam giác vuông, có một góc vuông (90 độ). Để tính diện tích tam giác vuông, chúng ta sử dụng công thức đơn giản nhất:
- Diện tích tam giác vuông = (cạnh góc vuông) x (độ dài cạnh kề) / 2
Diện tích tam giác bình thường
Trong tam giác bình thường (không vuông), chúng ta cần biết hai cạnh và góc giữa chúng. Để tính diện tích tam giác bình thường, chúng ta sử dụng công thức:
- Diện tích tam giác bình thường = (cạnh 1) x (cạnh 2) x sin(góc giữa hai cạnh) / 2
Diện tích tam giác đều
Tam giác đều là tam giác có ba cạnh bằng nhau. Để tính diện tích tam giác đều, chúng ta có một công thức đơn giản:
- Diện tích tam giác đều = (độ dài cạnh) ^ 2 x sqrt(3) / 4
Trong đó, sqrt(3) là ký hiệu của căn bậc hai của số 3.
Các công thức tính diện tích tam giác cơ bản này rất hữu ích và thường được sử dụng trong giáo dục và thực tế. Hiểu và áp dụng chúng giúp chúng ta tính toán diện tích tam giác một cách chính xác và nhanh chóng, từ những tam giác thông thường đến những tam giác đều đặc biệt.
Xem thêm: Công thức tính diện tích hình thang tổng hợp và đầy đủ nhất
Công thức Heron và tính diện tích tam giác không cần biết chiều cao
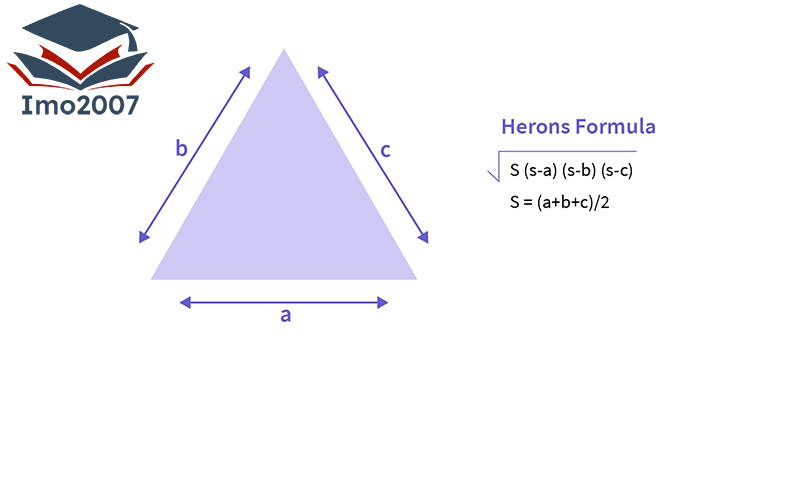
Giới thiệu về công thức Heron
Công thức Heron là một công thức tính diện tích hình tam giác dựa vào các cạnh của tam giác mà không cần biết chiều cao. Được đặt theo tên nhà toán học Heron của Alexandria, công thức này cũng được gọi là công thức Heron hoặc công thức Hero.
Cách tính diện tích tam giác bằng công thức Heron
Để tính diện tích tam giác ABC bằng công thức Heron, chúng ta cần biết độ dài của ba cạnh a, b và c. Công thức Heron được biểu diễn như sau:
- Diện tích tam giác ABC = sqrt(s * (s – a) * (s – b) * (s – c))
Trong đó, s là nửa chu vi của tam giác và được tính bằng công thức:
- s = (a + b + c) / 2
Ưu điểm và ứng dụng của công thức Heron
Công thức Heron là một công thức mạnh mẽ và linh hoạt cho phép tính diện tích tam giác dựa vào các cạnh mà không cần biết chiều cao. Công thức này rất hữu ích khi chúng ta không có thông tin về chiều cao hoặc không dễ dàng tính toán chiều cao của tam giác.
Ưu điểm chính của công thức Heron là tính chính xác và đơn giản, dễ dàng sử dụng trong các bài toán tính toán diện tích tam giác. Nó có ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, địa hình, định vị vị trí và trong các bài toán tư duy logic đòi hỏi tính toán diện tích tam giác một cách nhanh chóng và hiệu quả.
Tính diện tích tam giác thông qua định lý cosin và sin
Định lý cosin và cách tính diện tích tam giác thông qua nó
Định lý cosin là một trong những công cụ quan trọng để tính toán các hình học tam giác và chúng ta có thể sử dụng nó để tính diện tích tam giác khi biết ba cạnh và góc giữa hai cạnh. Định lý cosin nêu rõ mối quan hệ giữa bình phương của một cạnh của tam giác với tổng bình phương của hai cạnh còn lại và cosin của góc giữa hai cạnh đó.
Công thức tính diện tích hình tam giác ABC sử dụng định lý cosin là:
- Diện tích tam giác ABC = 1/2 * a * b * sin(C)
Trong đó, a và b là hai cạnh của tam giác, C là góc giữa hai cạnh a và b.
Định lý sin và cách tính diện tích tam giác thông qua nó
Định lý sin là công thức tính diện tích hình tam giác khi chúng ta biết hai cạnh và góc giữa chúng. Định lý sin nêu rõ mối quan hệ giữa một cạnh của tam giác với bán kính đường tròn ngoại tiếp tam giác và sin của góc đối diện với cạnh đó.
Công thức tính diện tích hình tam giác ABC sử dụng định lý sin là:
- Diện tích tam giác ABC = 1/2 * a * b * sin(C)
Trong đó, a và b là hai cạnh của tam giác, C là góc giữa hai cạnh a và b.
Cả hai định lý cosin và sin đều cung cấp những công thức tiện lợi để tính diện tích tam giác dựa vào các cạnh và góc của tam giác, và được sử dụng rộng rãi trong nhiều lĩnh vực, từ giáo dục đến thực tế, khi chúng ta cần tính toán diện tích tam giác một cách chính xác và hiệu quả.
Tính diện tích tam giác thông qua vectơ
Giới thiệu về tính diện tích tam giác dựa trên vectơ
Tính diện tích tam giác thông qua vectơ là một phương pháp tính diện tích hình tam giác sử dụng các đại lượng vectơ. Thay vì sử dụng độ dài cạnh và góc giữa các cạnh như trong các phương pháp truyền thống, phương pháp này dựa vào tích vector của hai cạnh của tam giác để tính diện tích.
Phương pháp tính diện tích tam giác bằng vectơ rất hữu ích trong không gian ba chiều khi tam giác có cạnh và đỉnh được biểu diễn dưới dạng vectơ. Nó cũng có thể được áp dụng trong không gian hai chiều khi chúng ta sử dụng vectơ pháp tuyến của các cạnh tam giác.
Công thức tính diện tích tam giác bằng vectơ
Để tính diện tích tam giác ABC thông qua vectơ, chúng ta sử dụng công thức sau:
- Diện tích tam giác ABC = 1/2 * |AB x AC|
Trong đó, AB và AC là hai vectơ cạnh của tam giác, “x” là phép nhân vectơ (tích vector), và |AB x AC| là độ dài của tích vector AB x AC.
Phương pháp tính diện tích tam giác bằng vectơ là một phương pháp hiệu quả và chính xác trong không gian ba chiều và có thể được áp dụng trong nhiều bài toán hình học và tính toán không gian phức tạp. Nó cũng mang tính ứng dụng cao trong lĩnh vực đồ họa máy tính, định vị GPS, và mô hình hóa không gian ba chiều.
Ứng dụng của công thức tính diện tích hình tam giác trong thực tế
Ứng dụng trong kiến trúc và xây dựng
Công thức tính diện tích hình tam giác rất hữu ích trong kiến trúc và xây dựng để tính toán diện tích các hình dạng tam giác trong các kết cấu và mô hình xây dựng. Khi thiết kế các mảnh đất, khu đô thị hoặc xây dựng các công trình như nhà ở, cầu, và tường chắn, tính diện tích tam giác giúp định rõ vị trí, kích thước và hình dạng của các bản đồ và kết cấu.
Ứng dụng trong định vị và đo lường
Công thức tính diện tích hình tam giác cũng được sử dụng trong định vị và đo lường địa lý. Trong định vị GPS, tính toán diện tích tam giác giúp xác định vị trí và khoảng cách giữa các địa điểm, đồng thời hỗ trợ lập bản đồ địa lý chính xác và phân tích các dự án cơ sở hạ tầng.
Ứng dụng trong vật lý và kỹ thuật
Trong vật lý, công thức tính diện tích hình tam giác được áp dụng để tính toán diện tích bề mặt, diện tích tiếp xúc giữa các đối tượng, diện tích dây, và các vấn đề liên quan đến lực, áp suất, và năng lượng.
Trong kỹ thuật, tính diện tích hình tam giác là một công cụ quan trọng để thiết kế các bản đồ mạch điện, tính toán diện tích mặt cắt của các thành phần máy móc, và phân tích diện tích tiếp xúc trong các ứng dụng liên quan đến cơ học và điện tử.
Tổng hợp lại, công thức tính diện tích hình tam giác có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của cuộc sống và ngành nghề, từ kiến trúc đến vật lý và kỹ thuật, đóng vai trò quan trọng trong việc giải quyết các vấn đề thực tế và cải thiện hiệu quả công việc.
Bài tập luyện tập tính diện tích tam giác
Bài tập về tính diện tích tam giác vuông
- Tính diện tích tam giác vuông có hai cạnh bằng 3 và 4 đơn vị.
- Một tam giác vuông có một cạnh bằng 5 và độ dài đường cao kẻ từ đỉnh vuông góc xuống đáy là 4. Tính diện tích tam giác.
Bài tập về tính diện tích tam giác bình thường
- Một tam giác ABC có các cạnh lần lượt là 6, 8 và 10 đơn vị. Tính diện tích tam giác.
- Cho tam giác có các cạnh a = 7, b = 9 và góc C giữa hai cạnh a và b là 45 độ. Tính diện tích tam giác.
Bài tập về tính diện tích tam giác đều
- Tính diện tích một tam giác đều có cạnh bằng 6 đơn vị.
- Một tam giác đều có bán kính đường tròn ngoại tiếp là 5 đơn vị. Tính diện tích tam giác.
Bài tập về tính diện tích hình tam giác sử dụng công thức Heron
- Tính diện tích hình tam giác có ba cạnh lần lượt là 8, 15 và 17 đơn vị bằng cách sử dụng công thức Heron.
- Cho tam giác có ba cạnh a = 7, b = 9 và c = 12 đơn vị. Tính diện tích tam giác bằng công thức Heron.
Bài tập về tính diện tích tam giác sử dụng định lý cosin và sin
- Một tam giác ABC có các cạnh lần lượt là 7, 10 và 12 đơn vị, góc A nằm giữa hai cạnh b và c là 60 độ. Tính diện tích tam giác.
- Tính diện tích tam giác có ba cạnh lần lượt là 5, 6 và 7 đơn vị, biết rằng góc giữa hai cạnh 5 và 6 là 45 độ.
Bài tập về tính diện tích tam giác dựa trên vectơ
- Cho tam giác có hai vectơ cạnh là AB = 3i + 2j và AC = i + 4j. Tính diện tích tam giác.
- Một tam giác có hai vectơ cạnh là AB = 2i + j và AC = 3i + 2j. Tính diện tích tam giác thông qua vectơ.
Đáp án:
- 1. Diện tích = 6 đơn vị vuông.
- Diện tích = 10 đơn vị vuông.
- 1. Diện tích = 24 đơn vị vuông.
- Diện tích ≈ 21.92 đơn vị vuông.
- 1. Diện tích ≈ 15.59 đơn vị vuông.
- Diện tích ≈ 21.65 đơn vị vuông.
- 1. Diện tích ≈ 60 đơn vị vuông.
- Diện tích ≈ 19.63 đơn vị vuông.
- 1. Diện tích ≈ 28.48 đơn vị vuông.
- Diện tích ≈ 11.03 đơn vị vuông.
- 1. Diện tích ≈ 4.5 đơn vị vuông.
- Diện tích ≈ 1.5 đơn vị vuông.
Xem thêm: Tính góc giữa hai đường thẳng: Khái niệm và phương pháp tính toán
Trong bài viết này, chúng ta đã tìm hiểu về công thức tính diện tích tam giác và các phương pháp tính diện tích tam giác thông qua định lý cosin, sin và công thức Heron. Chúng ta cũng đã thấy rõ ứng dụng của các công thức này trong nhiều lĩnh vực thực tế như kiến trúc, định vị, vật lý và kỹ thuật. Hẹn gặp lại trong các bài viết tiếp theo của imo2007 nhé