Trong thế giới hình học, tam giác là một khái niệm cơ bản và quen thuộc. Tuy nhiên, bên dưới vẻ đơn giản ấy lại tồn tại một điểm đặc biệt, một điểm giao nhau có tên gọi là “trọng tâm”. Trọng tâm của tam giác không chỉ đơn thuần là một điểm trong không gian, mà nó còn mang trong mình nhiều tính chất đặc trưng và ứng dụng thú vị. Chúng ta hãy cùng imo2007edu tìm hiểu qua bài viết dưới đây nhé!
Định Nghĩa Trọng Tâm của Tam Giác
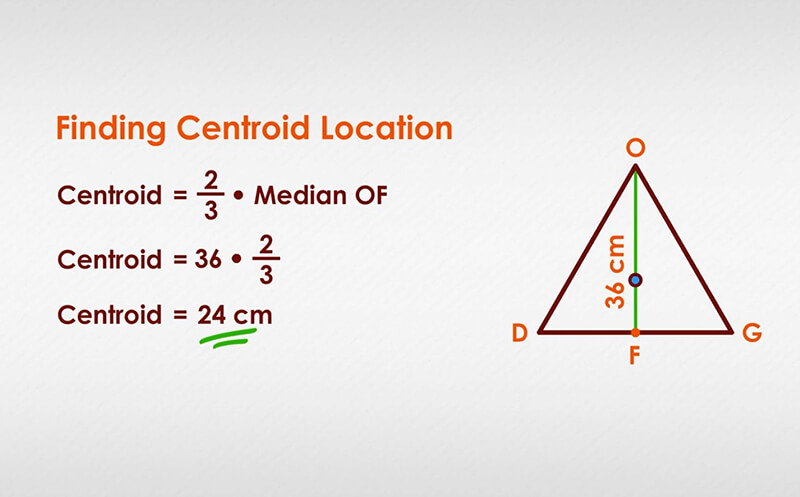
Trọng tâm của tam giác là một điểm đặc biệt đáng chú ý, là điểm giao nhau của ba đoạn thẳng kết nối từ mỗi đỉnh của tam giác đến trung điểm của cạnh đối diện. Điều này có nghĩa là khi ta vẽ đoạn thẳng từ một đỉnh đến trung điểm của cạnh đối diện, thì ba đoạn thẳng này sẽ cắt nhau tại một điểm duy nhất – điểm trọng tâm.
Vị Trí của Trọng Tâm Trong Tam Giác
- Trọng tâm luôn nằm bên trong tam giác, không bao giờ nằm ngoài tam giác.
- Nếu tam giác là tam giác đều (cạnh và góc của tam giác bằng nhau), thì trọng tâm trùng với tâm của đường tròn ngoại tiếp tam giác.
- Nếu tam giác có một cạnh là đoạn thẳng đứng, trọng tâm sẽ nằm trên cạnh này và chia tỷ lệ cạnh đứng theo tỷ lệ 2:1 từ đỉnh đối diện.
Trọng tâm không chỉ là điểm đặc biệt, mà còn có những tính chất đặc trưng và ứng dụng trong hình học và toán học. Việc hiểu rõ về trọng tâm sẽ giúp chúng ta khám phá nhiều điều thú vị về tam giác và các tính chất liên quan.
Tính Chất Quan Trọng của Trọng Tâm
Trọng tâm không chỉ đóng vai trò là điểm giao nhau của ba đoạn thẳng, mà còn có một số tính chất quan trọng khác:
Chia Tỷ Lệ Đoạn Thẳng
Trọng tâm chia các đoạn thẳng nối từ các đỉnh của tam giác đến trung điểm của cạnh đối diện theo tỷ lệ 2:1. Điều này có nghĩa là đoạn thẳng từ trọng tâm đến một đỉnh là gấp đôi đoạn thẳng từ trọng tâm đến trung điểm của cạnh đối diện.
Tính Chất Góc

Liên Hệ với Tâm Đường Tròn Nội Tiếp
Trọng tâm là một điểm đặc biệt liên quan đến tâm đường tròn nội tiếp tam giác. Đường tròn nội tiếp là đường tròn đi qua các đỉnh của tam giác và có tâm là điểm trọng tâm. Điều này đồng nghĩa với việc đường tròn nội tiếp tam giác cắt nhau tại điểm trọng tâm.
Những tính chất này giúp ta hiểu rõ hơn về vai trò quan trọng của trọng tâm và cách nó liên quan đến các yếu tố hình học khác trong tam giác.
Xem thêm: Khám Phá Định lý Cosin: Công Cụ Quan Trọng Trong Hình Học Tam Giác
Ứng Dụng Trọng Tâm trong Hình Học và Toán Học
Trọng tâm không chỉ là một khái niệm lý thuyết, mà còn có ứng dụng thực tiễn trong nhiều tình huống trong hình học và toán học. Dưới đây là một số cách chúng ta có thể áp dụng trọng tâm để giải quyết các bài toán thú vị:
Tối Ưu Hóa Tài Nguyên
Trọng tâm thể hiện sự cân bằng của tất cả các đỉnh và cạnh của tam giác. Điều này làm cho trọng tâm trở thành một điểm quan trọng trong việc tối ưu hóa việc phân chia tỷ lệ hoặc tài nguyên. Trong nhiều bài toán thực tế, chúng ta có thể sử dụng trọng tâm để xác định điểm tối ưu cho việc phân bổ tài nguyên, ví dụ như tối ưu hóa trọng lượng khi cân bằng các vật nặng trên một dây.
Phân Chia Diện Tích
Các đoạn thẳng từ trọng tâm đến các đỉnh tương ứng chia tam giác thành sáu phần tam giác nhỏ. Việc sử dụng trọng tâm để tính diện tích các phần tam giác nhỏ này có thể giúp chúng ta giải quyết các bài toán liên quan đến phân chia diện tích hoặc tỷ lệ trong các hình dạng phức tạp hơn.
Sự tương quan giữa trọng tâm và các phần khác của tam giác mở ra nhiều cơ hội cho việc áp dụng toán học vào thực tế, giúp chúng ta hiểu sâu hơn về các khía cạnh hình học và tối ưu hóa trong nhiều tình huống khác nhau.
Xem thêm: Khám Phá Diện Tích Hình Phẳng: Từ Cơ Bản Đến Phức Tạp
Bài Toán và Ví Dụ Minh Họa
Để hiểu rõ hơn về cách tính toán và áp dụng trọng tâm , hãy xem qua một số ví dụ cụ thể:
Ví Dụ 1: Tính Toán Trọng Tâm Giả sử ta có tam giác ABC với các đỉnh A(1,2), B(5,6), và C(9,2). Hãy tính toán tọa độ của trọng tâm G của tam giác này.

Ví Dụ 2: Ứng Dụng Trọng Tâm trong Thực Tế Một cửa hàng cần đặt một tượng hình tam giác lên mặt sàn để trang trí. Họ muốn đặt tượng sao cho trọng tâm của nó nằm chính giữa các góc của căn phòng. Tam giác căn phòng có các đỉnh A(0,0), B(10,0), và C(5,8). Hãy xác định tọa độ để đặt tượng.

Trọng tâm của tam giác là một điểm quan trọng trong hình học, không chỉ cho chúng ta hiểu về sự cân bằng của các đỉnh và cạnh mà còn có thể ứng dụng trong nhiều bài toán thực tế. Việc tính toán và áp dụng trọng tâm giúp chúng ta tối ưu hóa tài nguyên, phân chia tỷ lệ, và hiểu sâu hơn về các khía cạnh hình học. Hi vọng qua bài viết này của imo2007edu, bạn đã có cái nhìn rõ ràng về trọng tâm và cách nó gắn liền với thế giới xung quanh chúng ta.