Định lý cosin, còn được gọi là định lý cosin trong tam giác, là một trong những định lý quan trọng trong hình học tam giác. Nó liên quan đến mối quan hệ giữa các cạnh và góc của một tam giác không góc vuông. Trong bài viết này, imo2007 sẽ cùng các em tìm hiểu định lý này và vận dụng nó trong bài tập hình tam giác nhé.
Sự ra đời của định lí Cosin
Định lý Cosin được công bố lần đầu bởi nhà toán học Al-Kashi, còn được biết đến với tên gọi là định lý Al-Kashi, vào thế kỷ 15. Al-Kashi (1380 – 22/06/1429) là một nhà toán học nổi tiếng người Iran. Định lý Cosin được liên kết mật thiết với tên ông, và đây là một trong những đóng góp quan trọng của ông cho toán học.

Khái niệm của định lý Cosin có thể được hiểu là mở rộng của định lý Pythagore. Định lý Pythagore chỉ áp dụng cho tam giác vuông, giúp chúng ta tìm độ dài cạnh còn lại. Trong khi đó, định lý Cosin mở rộng áp dụng cho mọi tam giác, cho phép chúng ta xác định cạnh còn thiếu hoặc góc bên trong tam giác thường. Cụ thể, chúng ta có thể:
- Tìm độ dài cạnh của tam giác thường khi biết hai cạnh và góc giữa chúng.
- Xác định góc của một tam giác khi biết các cạnh của tam giác đó.
- Tìm độ dài cạnh thứ ba của một tam giác khi biết hai cạnh và góc đối diện với một trong hai cạnh đã biết.
Tóm lại, định lý Cosin là một công cụ mạnh mẽ trong hình học tam giác, giúp chúng ta khám phá các mối quan hệ phức tạp giữa các cạnh và góc của tam giác thường, không chỉ giới hạn trong trường hợp tam giác vuông như định lý Pythagore.
Định lí cosin
Định lý Cosin được sử dụng để tính độ dài của một cạnh của tam giác khi biết độ dài của hai cạnh khác và góc giữa chúng.
Định lý Cosin có dạng:
c² =a² +b²−2ab.cos(C)
Trong đó:
- là độ dài của cạnh đối diện góc .
- và là độ dài của hai cạnh khác, không phải cạnh đối diện góc .
- là giá trị của hàm cosin của góc (được tính theo độ).
Định lý cos được biểu diễn tương tự cho hai cạnh còn lại:
a² =b² +c²−2bc.cos(A)
b² =a² +c²−2ac.cos(B)
Định lý Cosin có thể được sử dụng trong nhiều tình huống khác nhau để tính toán các giá trị trong tam giác không góc vuông, ví dụ như tính độ dài cạnh, tính diện tích, và nhiều ứng dụng khác.
Vận dụng định lý cosin trong tam giác
Cho tam giác ABC, có AB = c, BC = a, AC = b, M là trung điểm BC. Tính độ dài đường trung tuyến AM theo a, b và c.
Phân tích bài toán:
Bài toán yêu cầu chúng ta tính độ dài của đoạn thẳng AM, và phương pháp thường được áp dụng để tính đoạn thẳng này là xem nó như là một cạnh của một hình giác nào đó.
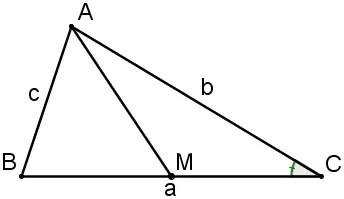
Theo đó, có hai lựa chọn cho chúng ta: chúng ta có thể coi AM là cạnh của tam giác ABM, hoặc coi nó là cạnh của tam giác ACM. Do hai tam giác này đều có vai trò quan trọng và tương đương nhau, chúng ta có thể lựa chọn bất kỳ cái nào trong hai tam giác này. Tôi sẽ chọn áp dụng tam giác ACM.
Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn CM = a/2 do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
![]()
Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.
![]()
Thay (2) vào (1), rồi rút gọn ta có kết quả
![]()
Trên đây là lý thuyết về định lí cosin và vận dụng của nó trong giải bài tập tam giác. Các em có thể tiếp tục ôn luyện dạng bài tập này trong sách bài tập toán cũng như các dạng đề thi cũ nhé.
