Trong hình học không gian, khái niệm “cát tuyến” là một khía cạnh thú vị và quan trọng. Cát tuyến không chỉ là một đường cong đơn giản, mà còn đầy ẩn chứa tính chất và ứng dụng đa dạng. Trên hành trình tìm hiểu về hình học không gian, chúng ta không thể bỏ qua khái niệm cát tuyến là gì và những điều thú vị mà nó mang lại. Hãy cùng imo2007eduvn khám phá khía cạnh hấp dẫn của cát tuyến trong bài viết này nhé.
Cát Tuyến là gì?
Cát tuyến là một khái niệm trong hình học không gian, thường được gọi là “đường cong không gian” hoặc “đường cong ba chiều”. Nó thể hiện một dãy các điểm không gian liên tiếp mà mỗi điểm trên đường cong đều được xác định bởi một tọa độ. Trong không gian ba chiều, cát tuyến có thể nằm trong không gian, không cần phải nằm trên một mặt phẳng.
Khái niệm cát tuyến là gì là một phần quan trọng của hình học không gian và có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, công nghệ, và kiến trúc. Cát tuyến có thể được sử dụng để mô hình hóa các đường cong phức tạp trong không gian thực tế và là một công cụ quan trọng trong việc nghiên cứu và giải quyết các vấn đề hình học phức tạp.
Xem thêm: Khám Phá Diện Tích Hình Phẳng: Từ Cơ Bản Đến Phức Tạp
Phương Trình Cát Tuyến – Từ Điểm Đến Hướng
Để xây dựng phương trình của cát tuyến, chúng ta cần biết ít nhất một điểm trên đường cong và hướng cát tuyến tại điểm đó. Hai yếu tố này là quan trọng để xác định một cát tuyến duy nhất trong không gian ba chiều.
Điểm Thuộc Cát Tuyến
Giả sử chúng ta biết một điểm trên cát tuyến. Điểm này đã được xác định và thuộc đường cong mà chúng ta đang quan tâm.
Hướng Cát Tuyến
Hướng cát tuyến tại điểm P cho biết sự biến đổi của đường cong tại điểm đó. Hướng cát tuyến có thể được biểu diễn bằng một vectơ đơn vị v=(a,b,c) trùng với hướng của đường cong tại P.
Xây Dựng Phương Trình: Với điểm thuộc cát tuyến và hướng cát tuyến tại điểm đó, chúng ta có thể xây dựng phương trình của cát tuyến. Phương trình của cát tuyến có thể được biểu diễn dưới dạng:
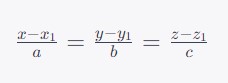
Trong đó, x,y,z là các biến đại diện cho điểm trên cát tuyến mà chúng ta đang xác định, và a,b,c là các thành phần của hướng cát tuyến tương ứng.
Phương trình cát tuyến cho phép chúng ta mô hình hóa và hiểu rõ hơn về đường cong trong không gian ba chiều thông qua các yếu tố quan trọng như điểm thuộc cát tuyến và hướng cát tuyến tại điểm đó.
Xem thêm: Khám Phá Định lý Cosin: Công Cụ Quan Trọng Trong Hình Học Tam Giác
Làm Quen Với Các Bài Toán Liên Quan Đến Cát Tuyến
Dưới đây là một số bài toán thực hành liên quan đến cát tuyến để bạn có cơ hội áp dụng kiến thức đã học vào thực tế. Đáp án cũng được cung cấp để bạn kiểm tra và tự đánh giá.

Mối Liên Hệ Giữa Cát Tuyến và Các Hình Khác Trong Không Gian
Cát tuyến không chỉ tồn tại riêng lẻ, mà còn có mối liên hệ chặt chẽ với nhiều hình học khác trong không gian như đường thẳng và mặt phẳng.
Mối Liên Hệ Với Đường Thẳng
Nếu một đường thẳng nằm hoàn toàn trên một cát tuyến, chúng ta nói rằng đường thẳng đó song song với cát tuyến. Điều này đồng nghĩa với việc hướng cát tuyến và hướng của đường thẳng này là như nhau hoặc nghịch đảo nhau.
Mối Liên Hệ Với Mặt Phẳng
Một cát tuyến có thể cắt qua một mặt phẳng trong không gian, tạo ra một đường cong chính là điểm giao giữa cát tuyến và mặt phẳng đó. Điều này thể hiện sự tương tác giữa cát tuyến và không gian bao quanh nó.
Tương Tác Phức Tạp Hơn
Mối liên hệ giữa cát tuyến, đường thẳng và mặt phẳng không dừng lại ở những mô hình đơn giản. Trong thực tế, chúng tạo nên những tương tác hình học phức tạp hơn, thúc đẩy sự tìm hiểu và áp dụng hình học không gian vào các vấn đề thực tế.
Nhìn chung, mối liên hệ giữa cát tuyến và các hình khác trong không gian giúp chúng ta hiểu sâu hơn về mối quan hệ hình học và cách chúng tương tác trong không gian ba chiều.
Chiến Thuật Học Hiệu Quả Về Cát Tuyến
Học về cát tuyến là một hành trình thú vị và cần sự kiên nhẫn. Dưới đây là một số chiến thuật giúp bạn học hiệu quả về cát tuyến:
Hiểu Rõ Cát Tuyến Là Gì
Bắt đầu bằng việc hiểu rõ khái niệm cơ bản về cát tuyến, phương trình cát tuyến, và hướng cát tuyến. Điều này giúp bạn xây dựng nền tảng vững chắc.
Thực Hành Nhiều Bài Tập
Giải nhiều bài toán thực hành liên quan đến cát tuyến để rèn luyện kỹ năng xây dựng phương trình và áp dụng kiến thức vào thực tế.
Áp Dụng Vào Vấn Đề Thực Tế
Khi bạn gặp các vấn đề thực tế liên quan đến không gian và hình học, hãy xem xét cách cát tuyến có thể áp dụng vào giải quyết vấn đề.
Sử Dụng Tài Liệu Tham Khảo
Sách giáo khoa, tài liệu học trực tuyến, và bài giảng trên mạng là những nguồn tài liệu hữu ích để nâng cao kiến thức về cát tuyến.
Bài viết đã cung cấp cái nhìn tổng quan về cát tuyến là gì và tầm quan trọng của nó trong không gian ba chiều. Chúng ta đã khám phá cách xây dựng và ứng dụng phương trình cát tuyến, mối liên hệ của nó với các hình học khác, cũng như chiến thuật học hiệu quả để nắm vững kiến thức. Sự hiểu biết về cát tuyến không chỉ giúp chúng ta giải quyết các vấn đề hình học phức tạp mà còn là nền tảng quan trọng trong việc hiểu và áp dụng kiến thức trong thế giới thực. Hẹn gặp lại các bạn trong các bài viết tiếp theo của imo2007eduvn nhé!