Kiến thức về nguyên hàm lượng giác đóng vai trò cực kỳ quan trọng trong chương trình toán cấp 3. Các công thức liên quan đến nguyên hàm lượng giác có nhiều mức độ khác nhau, từ những công thức cơ bản cho đến các công thức phức tạp hơn, cùng với sự đa dạng của các dạng bài tập tương ứng. Imo2007.edu.vn sẽ tổng hợp cho bạn các công thức cơ bản về nguyên hàm lượng giác cùng các công thức nâng cao hơn, cũng như cung cấp các ví dụ bài tập thực tế liên quan trong bài viết sau đây.
Các công thức lượng giác quan trọng cần nhớ
Bảng công thức nguyên hàm LG cơ bản
Bảng công thức nguyên hàm lượng giác hàm số hợp
Hàm số hợp u = u(x)
Hàm số hợp u = ax + b
6 dạng nguyên hàm lượng giác thường gặp và phương pháp giải
Dạng 1
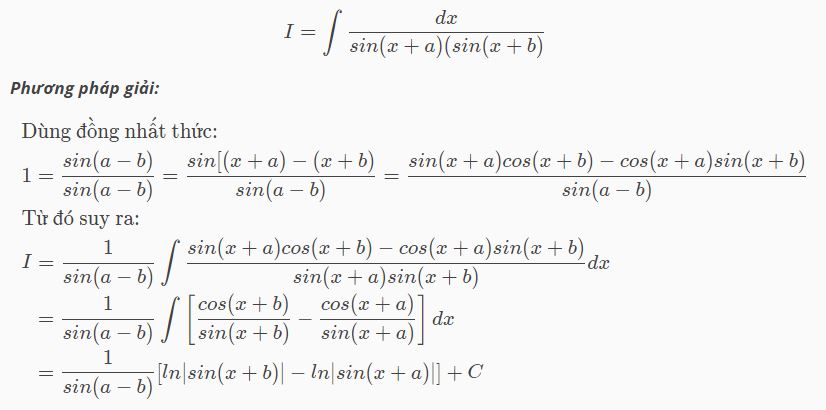
Dạng 2
Dạng 3
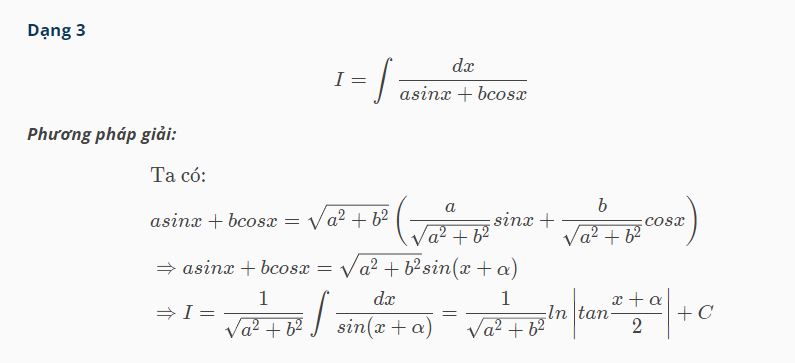
Dạng 4
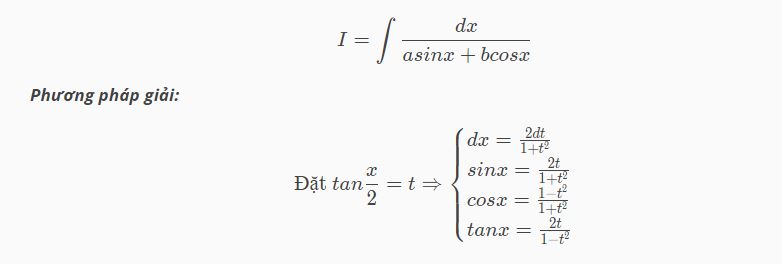
Dạng 5
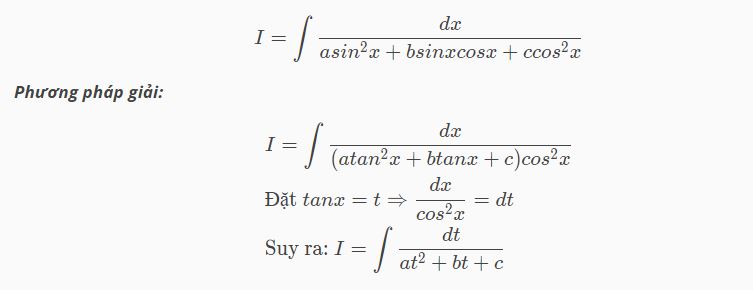
Dạng 6
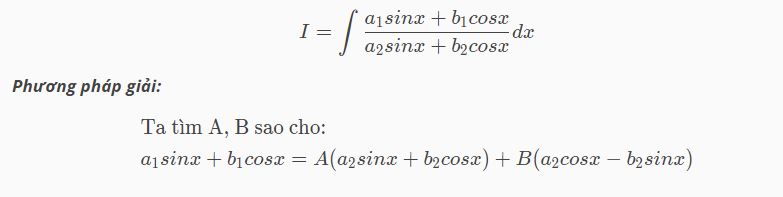
Những lưu ý khi làm bài tập dạng nguyên hàm lượng giác
- Kiến thức căn bản: Đảm bảo bạn đã hiểu rõ kiến thức căn bản về nguyên hàm và các công thức liên quan như công thức nguyên hàm của các hàm cơ bản (ví dụ: hàm mũ, hàm sin, hàm cos, hàm logarit) và luật tích phân.
- Tìm đạo hàm: Bắt đầu bằng việc tìm đạo hàm của hàm số trong bài tập. Điều này giúp bạn xác định hàm mà bạn đang cố gắng tích phân.
- Sử dụng công thức nguyên hàm: Áp dụng các công thức nguyên hàm thích hợp để tính toán. Điều này bao gồm công thức cơ bản cũng như công thức tích hợp và quy tắc chuỗi.
- Chú ý đến hằng số tích cực: Khi tích phân, đừng quên thêm hằng số tích cực (+C) vào kết quả cuối cùng. Điều này là quan trọng vì mỗi bài toán nguyên hàm sẽ có một hằng số tích cực khác nhau, tạo ra các hàm nguyên hàm khác nhau.
- Kiểm tra lại kết quả: Sau khi tích phân, hãy kiểm tra lại kết quả bằng cách đạo hàm ngược (lấy đạo hàm của hàm nguyên hàm) để đảm bảo kết quả của bạn đúng.
- Xem xét điều kiện giới hạn: Nếu bài tập yêu cầu xác định một khoảng giới hạn cho nguyên hàm, hãy đảm bảo bạn áp dụng giới hạn đúng cách để tính giá trị chính xác.
Chúc các em học tập thật tốt.
Xem thêm:
- Cách chứng minh 2 vecto vuông góc cực hay và dễ hiểu
- Cách tính độ dài véc tơ toán 10 đơn giản, có vận dụng dễ hiểu
