Hình thang là một hình rất hay gặp trong những bài tập về hình học, các em cần nắm vững công thức tính diện tích mỗi loại để khi muốn tính diện tích hình thang thì vận dụng ngay công thức tính toán phù hợp.
Cách tính diện tích hình thang
Hình thang là hình có 2 cạnh đáy song song và tổng tất cả các góc bằng 360 độ .Diện tích hình thang bằng trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy.
Cách tính diện tích của hình thang bất kỳ
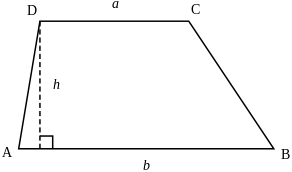
Để tính diện tích hình thang bất kỳ ta lấy trung bình cộng của 2 đáy nhân với chiều cao. Công thức cụ thể là:
S = h x (a + b)/2
Trong đó:
S là diện tích hình thang
a là độ dài đáy bé
b là độ dài đáy lớn
h là chiều cao của hình thang (khoảng cách giữa 2 cạnh đáy).
Mẹo ghi nhớ công thức:
“Muốn tính diện tích hình thang
Đáy lớn đáy bé ta mang cộng vào
Rồi đem nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra.”
Công thức tính diện tích hình thang vuông
Hình thang vuông là hình thang có một góc vuông và chiều cao chính bằng cạnh bên vuông góc với 2 đáy.
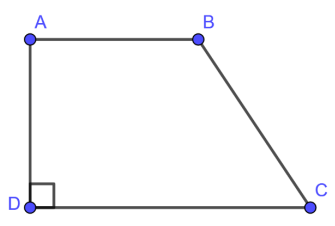
Áp dụng công thức tính diện tích hình thang bất kỳ ta có:
S = h x (a + b)/ 2 = AD x (AB + CD)/2
Trong đó:
S là diện tích của hình thang vuông.
a và b là độ dài của 2 cạnh đáy.
h là độ dài cạnh bên vuông góc với 2 đáy.
Công thức tính diện tích hình thang cân
Hình thang cân là một loại hình thang mà hai góc kề của một đáy bằng nhau, và hai cạnh bên cũng bằng nhau, như hình bên dưới. Để tính diện tích của hình thang cân, bạn có hai cách:
(1) Bạn có thể sử dụng công thức tính diện tích cho hình thang bất kỳ, như đã mô tả ở mục 1.
(2) Một cách khác là chia nhỏ hình thang thành các hình học nhỏ hơn, sau đó tính diện tích của từng phần và cộng chúng lại với nhau.
Cụ thể, hãy xem xét hình thang cân ABCD như trong hình dưới. Đường cao AH và BK chia hình thang thành một hình chữ nhật ABKH và hai hình tam giác ADH và BCK.
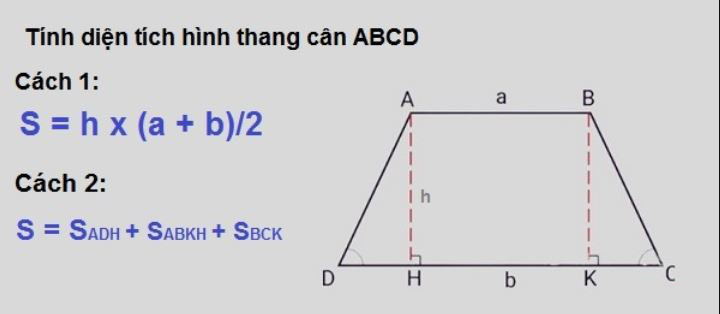
Để tính diện tích của hình thang ABCD, bạn có thể áp dụng công thức tính diện tích hình chữ nhật cho ABKH và công thức tính diện tích tam giác cho ADH và BCK. Sau đó, kết quả tính được từ các phần này sẽ được cộng lại với nhau để tìm diện tích tổng của hình thang ABCD.
Ví dụ minh hoạ
Cho một hình thang có chiều dài cạnh a = 20cm, cạnh b = 10cm và chiều cao nối từ đỉnh hình tháng xuống đáy là 8cm. Hỏi diện tích của hình thang là bao nhiêu?
Lời giải:
Áp dụng công thức tính diện tích của hình thang, ta có:
S = h x (a +b)/2 = 8 x (20+10)/2= 120 (cm²)
Vậy diện tích của hình thang trên là 120 (cm²)
Ví dụ 2: Có một mảnh đất hình thang với đáy bé là 48m, đáy lớn là 60m. Mở rộng hai đáy về phía bên phải của mảnh đất với đáy lớn thêm 14m, đáy nhỏ thêm 10m thu được mảnh đất hình thang mới với diện tích lớn hơn diện tích ban đầu là 72m2. Tính diện tích mảnh đất hình thang ban đầu.
Lời giải:
Theo đề bài, diện tích tăng thêm là diện tích hình thang có đáy lớn là 14m và đáy bé là 10m. Từ công thức tính diện tích của hình thang ta có:
h = (S x 2)/(a + b) = (72 x 2)/(14+10) = 6
Diện tích mảnh đất hình thang ban đầu là: S = 6 x (48 + 60)/2 = 324m²
Như vậy, bài viết trên đây đã giúp các em biết được muốn tính diện tích hình thang thì làm như thế nào rồi. Imo2007.edu.vn chúc các em học tập thật tốt nhé.
Xem thêm:
- Khám phá diện tích mặt cầu – Những điều cần biết
- Cách xác định góc giữa đường thẳng và mặt phẳng dễ hiểu nhất
