Nhị thức Newton đóng một vai trò quan trọng trong các kỳ thi lớp 11 và kỳ thi Trung học phổ thông Quốc gia. Bài viết này về cuộc thi IMO2007 sẽ giúp học sinh hiểu sâu về lý thuyết và các loại bài tập liên quan, bao gồm: cách khai triển nhị thức newton, xác định số hạng trong phân tích nhị thức, tính tổng của chúng, thực hiện các phép rút gọn biểu thức, chứng minh các biểu thức, giải phương trình và bất phương trình, và áp dụng nhị thức Newton trong các bài toán liên quan đến tổ hợp và tổ hợp hoán vị, thông qua một loạt các ví dụ minh họa.
Tìm hiểu lý thuyết nhị thức newton
Định lý khai triển nhị thức niu tơn
Trong chương trình toán giải tích lớp 11, chúng ta đã học về một định lý quan trọng trong toán học, đó là Định lý Khai triển Nhị thức Newton, ngắn gọn gọi là Định lý Nhị thức. Đây là một định lý quan trọng về việc khai triển hàm mũ của tổng. Định lý này cho biết cách khai triển một nhị thức bậc n thành một đa thức có tổng cộng n+1 số hạng.
Công thức nhị thức niu tơn
Định lý
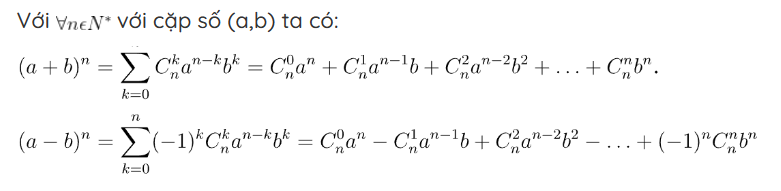
Hệ quả
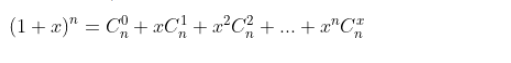
Cách khai triển nhị thức newton
Cách tìm hệ số và tìm số hạng trong khai triển nhị thức newton
Trong loại bài toán này, các bạn cần sử dụng số hạng tổng quát (số hạng thứ k+1) của quá trình khai triển. Sau đó, thực hiện biến đổi để phân tách phần biến và phần hệ số, sau đó kết hợp với thông tin trong đề bài để xác định giá trị của chỉ số k. Lưu ý rằng số hạng bao gồm cả phần hệ số và phần biến.
Ví dụ cách tìm hệ số trong khai triển
Ví dụ cách tìm số hạng trong khai triển
Giải phương trình, bất phương trình chỉnh hợp tổ hợp
Trong loại bài toán này, bạn cần áp dụng các công thức tính số hoán vị, tổ hợp, và chỉnh hợp để biến đổi phương trình. Sau đó, hãy kiểm tra điều kiện của các nghiệm và rút ra kết luận từ đó.
Trên đây là toàn bộ lý thuyết và các dạng bài tập liên quan đến khai triển nhị thức Newton trong chương trình Toán lớp 11. Để đạt được điểm số cao, các em nên thực hành nhiều dạng bài tập khác nhau. Hy vọng rằng thông qua bài viết này, các em sẽ có khả năng giải quyết các loại bài từ những bài cơ bản đến những bài tập phức tạp nhằm phục vụ cho kỳ thi tốt nghiệp THPTQG.
Xem thêm:
- Nguyên hàm lượng giác là gì? Bảng tổng hợp nguyên hàm của hàm số lượng giác
- Cách chứng minh 2 vecto vuông góc cực hay và dễ hiểu
