Để đảm bảo thành công trong việc học tam thức bậc hai, điều quan trọng là hiểu vững lý thuyết và có khả năng giải quyết nhiều dạng bài tập. imo2007 đã tổng hợp kiến thức về tam thức bậc hai trong môn Toán lớp 10, bao gồm cách xác định dấu của nó và cách áp dụng, tất cả được trình bày trong bài viết dấu của tam thức bậc hai dưới đây. Điều này sẽ giúp các bạn nắm vững nội dung này và có cơ hội đạt được điểm cao trong học tập.

Dấu của tam thức bậc hai là gì?
Tam thức bậc hai (quadratic equation) là một phương trình bậc hai trong biến số , có dạng tổng quát là:
ax² + bx+ c =0
Trong đó:
- , , và là các hệ số có thể là các số thực hoặc số phức.
- là biến số mà chúng ta cố gắng tìm ra giá trị thỏa mãn phương trình.
Dấu của tam thức bậc hai phụ thuộc vào giá trị của biểu thức b² − 4ac, được gọi là delta (). Cụ thể:
- Nếu , tức là delta lớn hơn 0, thì tam thức có hai nghiệm thực phân biệt.
- Nếu , tức là delta bằng 0, thì tam thức có một nghiệm kép (nghiệm trùng nhau).
- Nếu , tức là delta nhỏ hơn 0, thì tam thức không có nghiệm thực, nhưng có nghiệm phức.
Dấu của tam thức bậc hai có thể giúp xác định số lượng và tính chất của các nghiệm của phương trình.
Bất phương trình bậc hai một ẩn
Bất phương trình bậc hai là gì?
Bất phương trình bậc hai một ẩn x là bất phương trình có dạng:
ax² + bx + c < 0
ax² + bx + c ≤ 0
ax² + bx + c > 0
ax² + bx + c ≥ 0
Trong đó, a, b, c là những số thực và a ≠ 0.
Cách giải bất phương trình bậc hai
Để giải bất phương trình bậc hai một ẩn ax² + bx + c < 0, các em cần phải tìm các khoảng mà trong đó:
f(x) = ax² + bx + c cùng dấu với hệ số a (a < 0)
f(x) = ax² + bx + c trái dấu với hệ số a (trường hợp a > 0)
Bài tập minh họa cho dấu của tam thức bậc hai
Bài 1: Xét dấu tam thức bậc hai: -2x² + 3x + 5
Tam thức −2x² + 3x + 5 có Δ= 9+40 = 49 >0 Tam thức có hai nghiệm phân biệt là x1 = –1 và x2 = 25, hệ số a= –2 <0
Chúng ta có thể lập bảng xét dấu như sau:
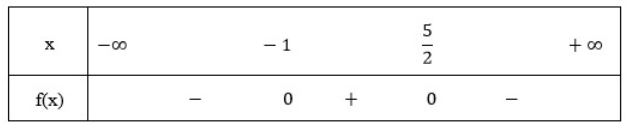
Bài 2: Giải bất phương trình bậc hai: 4x² – x + 1 < 0
Cách giải:
Xét tam thức f(x) = 4x² – x + 1 có Δ = -15 < 0; a = 4 > 0 nên f(x) > 0 ∀x ∈ R
Vậy bất phương trình 4x² – x + 1 < 0 vô nghiệm.
Những lưu ý khi giải bài tập dạng tam thức bậc hai
- Đọc hiểu bài toán: Đầu tiên, hãy đọc hiểu kỹ đề bài để biết chính xác những gì đang được yêu cầu. Xác định các thông tin quan trọng như giá trị của các hệ số , , và , và mục tiêu cần tìm, ví dụ: xác định dấu của nghiệm, tìm giá trị của khi thỏa mãn điều kiện nào đó, vv.
- Sử dụng công thức Δ (Delta): Để xác định dấu của tam thức bậc hai, sử dụng công thức Δ=, nơi Δ là delta, , và là các hệ số của phương trình . Kết quả của sẽ cho biết tam thức có bao nhiêu nghiệm và tính chất của chúng.
- : Nếu , tam thức có hai nghiệm thực và phân biệt. Bạn có thể sử dụng công thức nghiệm của tam thức bậc hai để tính nghiệm chính xác.
- : Nếu , tam thức có một nghiệm kép (nghiệm trùng nhau). Lúc này, bạn có thể sử dụng công thức nghiệm kép để tính giá trị của nghiệm.
- : Nếu , tam thức không có nghiệm thực. Tuy nhiên, nó có nghiệm phức. Bạn có thể sử dụng số phức để biểu diễn nghiệm.
- Lưu ý về các dấu trong kết quả: Khi xác định dấu của nghiệm, hãy kiểm tra cẩn thận dấu của từng phần tử trong công thức delta và trong công thức nghiệm để đảm bảo tính chính xác.
Trên đây, imo2007 đã cung cấp những kiến thức quan trọng và minh họa về tam thức bậc hai trong môn Toán lớp 10. Hãy duy trì việc theo dõi chúng tôi hàng ngày để tiếp tục học thêm nhiều bài học thú vị về Toán học. Chúc các em đạt được thành công đáng kể trong học tập của mình!
Xem thêm: