Hàm số logarit và công thức tính đạo hàm của logarit là những khái niệm quan trọng mà các em học sinh sẽ tiếp cận trong chương trình Toán lớp 12. Những kiến thức này không chỉ có vai trò quan trọng trong việc hiểu sâu hơn về toán học mà còn thường xuất hiện trong các bài thi quan trọng. Do đó, imo2007 sẽ tổng hợp lại những kiến thức cơ bản liên quan đến hàm logarit, cách tính đạo hàm log cùng với những ví dụ minh họa, nhằm giúp các em nắm vững phần kiến thức này.
Nắm vững các công thức đạo hàm

Những quy tắc cơ bản của đạo hàm
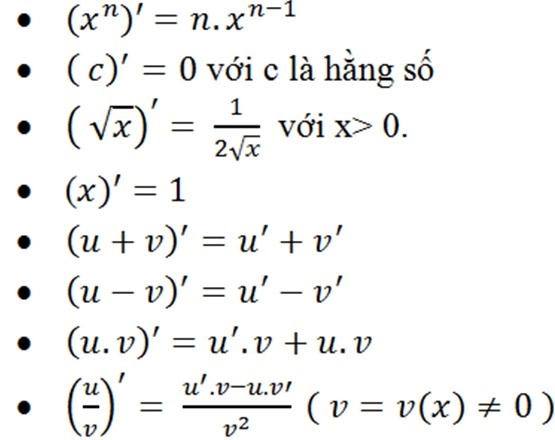
Bảng đạo hàm lượng giác

Bảng công thức đạo hàm logarit

Công thức đạo hàm số mũ

Công thức đạo hàm log
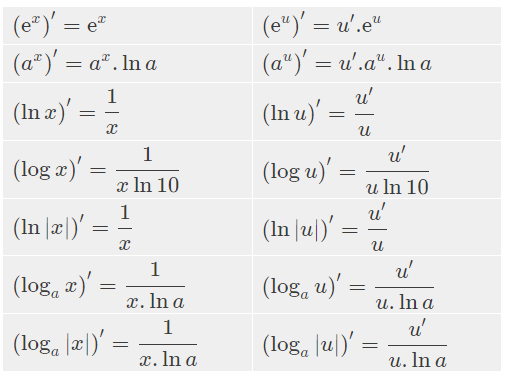
Xem thêm: Tổng hợp đầy đủ công thức logarit lớp 12 cần nắm
Bảng đạo hàm và nguyên hàm
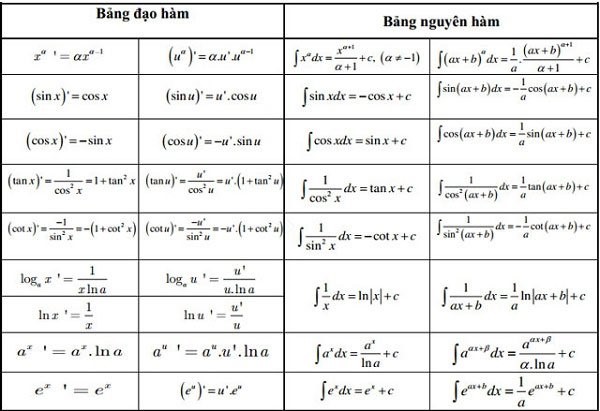
Tổng hợp một số dạng bài toán về công thức đạo hàm
Tính đạo hàm bằng định nghĩa
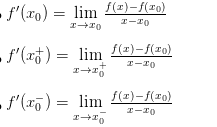
Hàm số y = f(x) có đạo hàm tại điểm x= x <=> f'(x )=f'(x )
Hàm số y = f(x) có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.
Ví dụ 1: f(x) = 2x +1 tại x=2
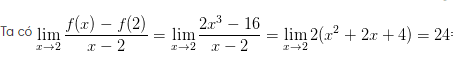
Chứng minh các đẳng thức về đạo hàm
Ví dụ 2: Xét hàm số y = ln(x^2). Chứng minh rằng y”’ – 2y” + 4y’ – 4y = 0.
Bài giải:
Bước 1: Tính các đạo hàm cần thiết của hàm số y = ln(x^2).
y’ = 2x * (1/x^2) = 2/x,
y” = -2/x^2,
y”’ = 4/x^3.
Bước 2: Thay các giá trị đạo hàm vào phương trình cần chứng minh.
y”’ – 2y” + 4y’ – 4y = 4/x^3 – 2*(-2/x^2) + 4*(2/x) – 4ln(x^2)
= 4/x^3 + 4/x^2 + 8/x – 4ln(x^2)
= 4/x^2 * (1/x + 1) + 8/x – 4ln(x^2)
= 4/x^2 * (x+1) + 8/x – 4ln(x^2).
Bước 3: Rút gọn biểu thức và chứng minh điều kiện.
4/x^2 * (x+1) + 8/x – 4*ln(x^2)
= 4 * (x+1) + 8x^(-1) – 8ln(x^2)
= 4x + 4 + 8/x – 8ln(x^2)
= 4x – 8ln(x^2) + 4 + 8/x.
Bởi vì ln(x^2) = 2ln(x), ta có thể viết lại thành: 4x – 16ln(x) + 4 + 8/x.
Vậy, y”’ – 2y” + 4y’ – 4y = 0 đã được chứng minh.
Viết phương trình tiếp tuyến khi biết tiếp điểm
Ví dụ: Xét hàm số y = 2x^2 + mx + (m – 1)x + 3, với m là một tham số thực. Tìm giá trị của m sao cho đường tiếp tuyến của đồ thị hàm số này tại điểm có hoành độ x = 2 đi qua điểm B(3, 10).
Bài giải:
Bước 1: Tính đạo hàm của hàm số y = 2x^2 + mx + (m – 1)x + 3. y’ = 4x + m + m – 1 = 4x + 2m – 1.
Bước 2: Tìm độ dốc của tiếp tuyến tại điểm M(2, y(M)) và viết phương trình tiếp tuyến. Ở điểm M(2, y(M)), ta có y(M) = 2(2)^2 + m(2) + (m – 1)(2) + 3 = 8 + 2m + 2m – 2 + 3 = 12 + 4m. Và y'(2) = 4(2) + 2m – 1 = 8 + 2m – 1 = 2m + 7.
Phương trình tiếp tuyến tại điểm M(2, y(M)) là: y = (2m + 7)(x – 2) + (12 + 4m).
Bước 3: Điều kiện để điểm B(3, 10) nằm trên tiếp tuyến đã tìm. Thay x = 3 và y = 10 vào phương trình tiếp tuyến: 10 = (2m + 7)(3 – 2) + (12 + 4m), 10 = 2m + 7 + 12 + 4m, 26 = 6m, m = 26/6, m = 13/3.
Vậy, để đường tiếp tuyến của đồ thị hàm số đi qua điểm B(3, 10), thì giá trị của m cần thỏa mãn là m = 13/3.
Viết phương trình tiếp khi biết hệ số góc
Viết PTTT Δ của ( C ) : y = f( x ), biết Δ có hệ số góc k cho trước
Gọi M( x ;y ) là tiếp điểm. Tính y’ => y'(x )
Do phương trình tiếp tuyến Δ có hệ số góc k => y’ = ( x ) = k (i)
Giải (i) tìm được x => y = f(x ) => Δ : y = k (x – x )+ y
Lưu ý: Hệ số góc k = y'( x ) của tiếp tuyến Δ thường cho gián tiếp như sau:
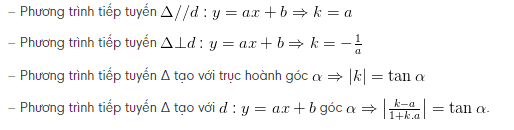
Ví dụ: Cho hàm số y=x +3x -9x+5 ( C). Trong tất cả các tiếp tuyến của đồ thị ( C ), hãy
tìm tiếp tuyến có hệ số góc nhỏ nhất.
Ta có y’ = f'( x ) = 3x + 6x – 9
Gọi x là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x ) = 3 x + 6 x – 9
Ta có 3 x + 6 x – 9 =3 ( x + 2x +1) – 12 = 3 (x +1) – 12 > – 12
Vậy min f( x )= – 12 tại x = -1 => y =16
Suy ra phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4
Phương trình và bất phương trình có đạo hàm

Imo2007 vừa cung cấp cho các em những thông tin quan trọng liên quan đến hàm logarit và cách tính đạo hàm log. Hy vọng rằng bài viết này có thể trang bị cho các em những kiến thức cơ bản quan trọng, giúp các em nâng cao hiểu biết toán học và đạt kết quả tốt trong các kỳ thi sắp tới.