Chủ đề về nguyên hàm của các hàm lượng giác là một phần quan trọng trong chương trình Toán Giải tích lớp 12. Các hàm lượng giác cơ bản sẽ có các công thức cụ thể để tính nguyên hàm, trong khi một số hàm phức tạp hơn đòi hỏi phải sử dụng phương pháp biến đổi trước khi áp dụng công thức để giải các bài tập. Dưới đây, imo2007.edu.vn sẽ hướng dẫn các em cách tính nguyên hàm tanx và cung cấp một số ví dụ để giải các bài tập thực tế, giúp các em củng cố kiến thức một cách hiệu quả hơn.
Ôn lại công thức tính nguyên hàm của hàm số lượng giác cơ bản
Trước khi đi đến vấn đề chính, các em phải củng cố lại các công thức nguyên hàm của hàm số lượng giác cơ bản thông qua bảng dưới đây:
Cách tính nguyên hàm tanx
Thực tế là không tồn tại một công thức cụ thể để tính. Thay vào đó, chúng ta cần dựa vào bảng công thức nguyên hàm cơ bản đã được trình bày ở trên để biến đổi và tính toán nguyên hàm của hàm tanx:
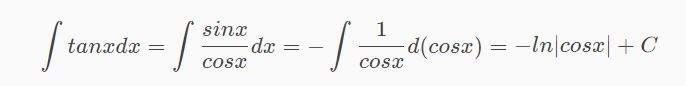
Cách giải bài tập nguyên hàm tanx
Trong bài tập về nguyên hàm của hàm tanx, các em cần thực hiện một loạt bước. Đầu tiên, các em cần phải biến đổi bài toán để chuyển nó thành dạng nguyên hàm của một trong các hàm lượng giác cơ bản. Sau đó, các em có thể áp dụng các công thức nguyên hàm đã biết để tìm kết quả. Bên cạnh đó, để giải quyết các dạng bài tập phức tạp hơn, các em cũng có thể áp dụng hai phương pháp biến đổi hàm hợp nâng cao dưới đây.
Dạng 1: Tính nguyên hàm tanx bằng phương pháp đổi biến t = u(x)
Bước 1: Đặt t = u(x)
Bước 2: Tính vi phân 2 vế dt = u'(x)dx.
Bước 3: Biến đổi hàm số f(x)dx = g(t)dt.
Bước 4: Tính ∫f(x)dx = ∫g(t)dt = G(t) + C = G(u(x)) + C.
Dạng 2: Tính nguyên hàm tanx bằng phương pháp đổi biến x = u(t)
Bước 1: Đặt x = u(t)
Bước 2: Tính vi phân 2 vế dx = u'(t)dt.
Bước 3: Biến đổi hàm số f(x)dx = f(u(t)).u'(t).dt = g(t)dt
Bước 4: Tính ∫f(x)dx = ∫g(t)dt = G(t) + C
Bài tập áp dụng
Bài 1: Tìm nguyên hàm của hàm số y = f(x) = tan2x trên tập số thực ta thu được kết quả:
Hướng dẫn giải
Ta có: y = f(x) = tan2x = tanx.(1 + tan2x) – tanx
Khi đó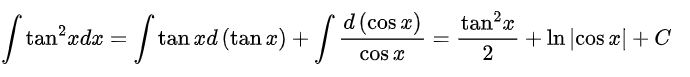 
Đáp án A
Bài 2: Nguyên hàm hàm y = (tanx)8
Hướng dẫn giải
Các công thức nguyên hàm liên quan đến hàm lượng giác thật sự không quá khó nếu các em thực sự tập trung và ôn tập chăm chỉ. Chúng tôi hy vọng rằng kiến thức về nguyên hàm của hàm tanx và các bài tập đã chia sẻ ở đây sẽ giúp các em hiểu sâu hơn về chủ đề này và đạt được điểm cao hơn trong các kỳ thi toán sắp tới.
Xem thêm:
- Đạo hàm arctan là gì? Công thức và quy tắc quan trọng cần nhớ
- Định lý cosin và vận dụng định lí cosin trong tam giác
