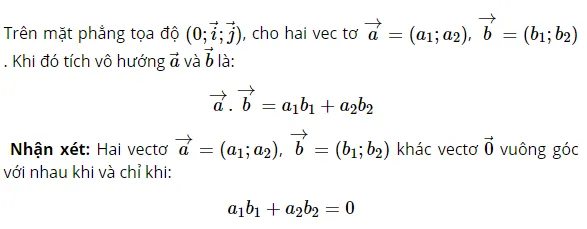Tích Vô Hướng của 2 Vecto là gì ? Định Nghĩa, Tính Chất, Công Thức
Tích vô hướng là khái niệm trang bị cho một không gian vectơ H trên trường K (K là trường số phức hay số thực) để có thể biến nó thành một không gian Hilbert. Đó là một hàm 2 biến như sau:
Thỏa mãn 4 tiên đề sau:
Đây là tiên đề hóa để xây dựng khái niệm tích vô hướng từ một số tính chất cơ bản của tích vô hướng thông thường của 2 vectơ hình học trong mặt phẳng (hay không gian) nhằm mô tả khái niệm góc (trực giao) của 2 vectơ trong một không gian vectơ trừu tượng.
Nội Dung
Tích vô hướng của hai vecto là gì ?
1. Định nghĩa
2. Tính chất
Người ta chứng minh được các tính chất sau đây của tích vô hướng :