Trong hình học không gian, khối trụ là một trong những hình học phổ biến và có nhiều ứng dụng trong cuộc sống và công nghiệp. Trong bài viết này, các bạn hãy cùng với imo2007eduvn khám phá về thể tích khối trụ, định nghĩa cũng như cách tính toán một cách dễ dàng và hiệu quả. Hãy cùng tìm hiểu chi tiết!
Khái niệm và công thức tính thể tích khối trụ
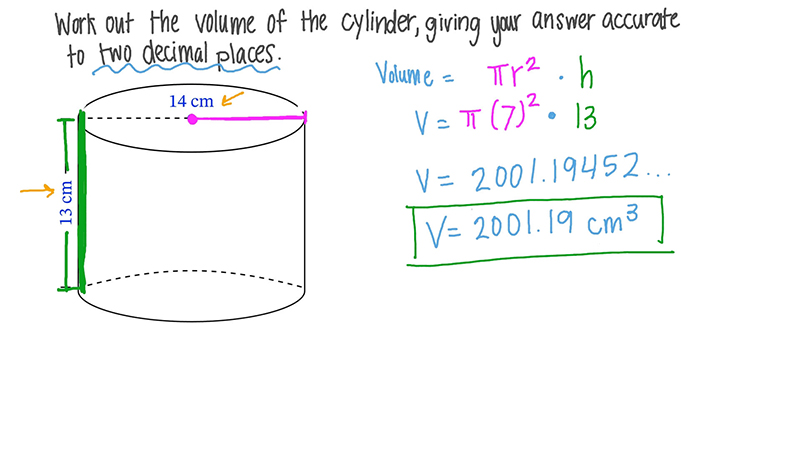
Định nghĩa thể tích hình trụ là gì?
Thể tích khối trụ là một khái niệm trong hình học không gian, dùng để đo lường dung tích không gian bên trong một khối trụ. Khối trụ là một hình học có đáy và đỉnh nằm trên một trục thẳng, với các cạnh là các đoạn thẳng kết nối đỉnh và các điểm của đáy. Thể tích hình trụ đóng vai trò quan trọng trong nhiều bài toán học tập và thực tế, như trong công nghiệp, xây dựng, thiết kế vật thể, và nhiều lĩnh vực khác.
Công thức tính thể tích hình trụ
Công thức tính thể tích khối trụ là:
- V = π * r^2 * h
Trong đó:
- V là thể tích hình trụ,
- π (pi) là hằng số số π (khoảng 3.14159),
- r là bán kính đáy của trụ,
- h là chiều cao của trụ.
Giải thích ý nghĩa và công thức từng thành phần trong tính toán
Công thức tính thể tích khối trụ dựa trên việc tính diện tích của đáy và nhân với chiều cao của trụ. Diện tích đáy của trụ là diện tích hình tròn, được tính bằng công thức π * r^2, trong đó r là bán kính đáy. Sau đó, chúng ta nhân diện tích đáy với chiều cao h để tính ra thể tích toàn bộ của khối trụ.
Công thức này giúp chúng ta tính toán một cách hiệu quả thể tích của một khối trụ với bán kính đáy và chiều cao đã biết. Sử dụng công thức này, chúng ta có thể áp dụng vào nhiều bài toán thực tế và học tập một cách dễ dàng và chính xác.
Xem thêm: Khám phá thể tích khối nón và cách tính toán đơn giản
Ví dụ và bài tập thực hành

Tính thể tích hình trụ trong các bài toán cụ thể
Ví dụ 1: Một thùng trụ có bán kính đáy là 5cm và chiều cao là 12cm. Hãy tính thể tích của thùng trụ này.
- Giải: Thể tích khối trụ V = π * r^2 * h = 3.14159 * 5^2 * 12 ≈ 942.48cm³ (kết quả được làm tròn đến 2 chữ số thập phân).
Ví dụ 2: Một cột trụ có bán kính đáy là 7cm và chiều cao là 20cm. Hãy tính thể tích của cột trụ này.
- Giải: Thể tích hình trụ V = π * r^2 * h = 3.14159 * 7^2 * 20 ≈ 3086.48cm³ (kết quả được làm tròn đến 2 chữ số thập phân).
Thực hành tính toán với các dạng khối trụ khác nhau
- Bài tập 1: Một hộp trụ có bán kính đáy là 6cm và chiều cao là 15cm. Hãy tính thể tích của hộp trụ này.
- Bài tập 2: Một cột trụ có bán kính đáy là 10cm và chiều cao là 25cm. Hãy tính thể tích của cột trụ này.
- Bài tập 3: Một hũ trụ có bán kính đáy là 8cm và chiều cao là 18cm. Hãy tính thể tích của hũ trụ này.
Đáp án:
- Bài tập 1: Thể tích hình trụ V = π * r^2 * h = 3.14159 * 6^2 * 15 ≈ 1696.53cm³ (kết quả được làm tròn đến 2 chữ số thập phân).
- Bài tập 2: Thể tích hình trụ V = π * r^2 * h = 3.14159 * 10^2 * 25 ≈ 7853.98cm³ (kết quả được làm tròn đến 2 chữ số thập phân).
- Bài tập 3: Thể tích khối trụ V = π * r^2 * h = 3.14159 * 8^2 * 18 ≈ 3627.43cm³ (kết quả được làm tròn đến 2 chữ số thập phân).
Hãy thực hành tính toán với các bài tập trên để rèn luyện kỹ năng tính toán thể tích hình trụ và hiểu rõ hơn về cách áp dụng công thức vào các dạng khối trụ khác nhau.
Lưu ý khi tính toán thể tích khối trụ
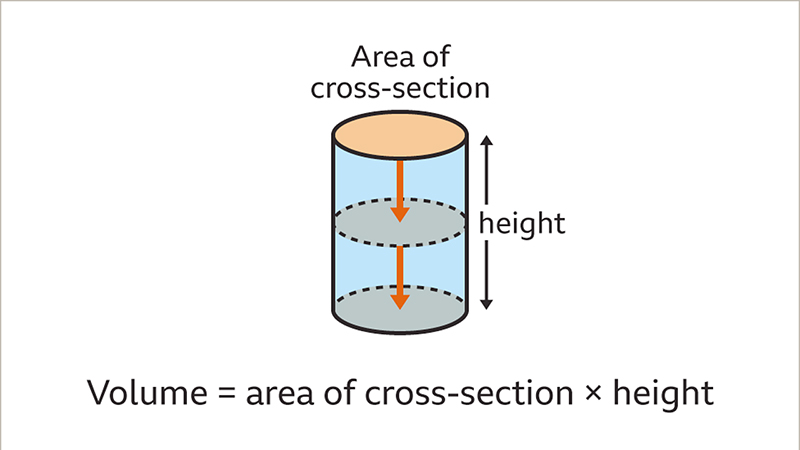
Xác định đơn vị đo và cách làm tròn kết quả
Trước khi tiến hành tính toán thể tích hình trụ, hãy xác định rõ đơn vị đo cho bán kính và chiều cao của khối trụ. Đảm bảo sử dụng cùng một đơn vị đo cho toàn bộ bài toán để tránh sai sót trong quá trình tính toán.
Khi hoàn thành phép tính, hãy làm tròn kết quả tính toán sao cho phù hợp với độ chính xác cần thiết. Thông thường, kết quả được làm tròn đến 2 hoặc 3 chữ số thập phân tùy vào độ chính xác yêu cầu trong bài toán.
Cách tránh các sai sót phổ biến khi tính toán
Để tránh sai sót khi tính toán thể tích khối trụ, hãy chú ý đến những điểm sau:
- Sai số đo lường: Kiểm tra kỹ các giá trị đo lường của bán kính và chiều cao của khối trụ. Sai số trong đo lường có thể dẫn đến kết quả tính toán không chính xác.
- Lỗi tính toán: Cẩn thận trong quá trình thực hiện phép tính. Một lỗi nhỏ trong quá trình tính toán có thể dẫn đến sai sót lớn trong kết quả cuối cùng.
Sử dụng công cụ hỗ trợ và ứng dụng tính toán thể tích hình trụ
Để tăng hiệu quả và độ chính xác trong tính toán thể tích khối trụ, hãy sử dụng các công cụ hỗ trợ như máy tính hoặc ứng dụng tính toán trên điện thoại di động. Các ứng dụng tính toán thể tích hình trụ đã tích hợp sẵn công thức và quy trình tính toán, giúp bạn thực hiện phép tính nhanh chóng và chính xác.
Ứng dụng công cụ hỗ trợ giúp tiết kiệm thời gian và giảm thiểu sai sót trong quá trình tính toán. Ngoài ra, tích hợp công cụ tính toán vào thực tế và công nghiệp giúp bạn giải quyết nhanh chóng các bài toán liên quan đến thể tích hình trụ trong các lĩnh vực khác nhau.
Xem thêm: Cách xác định góc giữa 2 vecto cực hay và chi tiết
Tính toán thể tích hình trụ là một khái niệm quan trọng trong hình học không gian, đóng vai trò quan trọng trong nhiều lĩnh vực cuộc sống và công nghiệp. Qua bài viết này, chúng ta đã nắm vững công thức tính thể tích khối trụ và hiểu rõ ý nghĩa từng thành phần trong phép tính. Các bạn hãy luyện tập thêm để thành thạo công thức này nhé, hẹn gặp lại các bạn trong các bài viết tiếp theo của imo2007eduvn!