Nguyên hàm của ln x là gì? Cách giải các dạng bài tập ln x

Bài tập về việc tính nguyên hàm của ln x thường khiến nhiều học sinh gặp khó khăn và mất điểm. Để đảm bảo bạn có điểm tối đa cho phần này, bạn cần hiểu rõ công thức và rèn luyện bằng cách giải nhiều dạng bài tập khác nhau. Dưới đây, imo2007.edu.vn sẽ chia sẻ một bài viết hữu ích giúp bạn không bị mất điểm ở phần này.

Mục lục

1. Định nghĩa nguyên hàm của ln x

2. Bảng công thức nguyên hàm của ln(x)

3. Cách tính nguyên hàm của ln x

4. Ví dụ minh hoạ

5. Những ứng dụng trong đời sống của ln x

Định nghĩa nguyên hàm của ln x

Nguyên hàm của hàm số ln(x), thường được ký hiệu là ∫ln(x)dx, là một hàm số F(x) mà khi bạn tích phân nó theo biến x, bạn sẽ thu được hàm số ln(x) ban đầu. Tức là:

∫ln(x)dx = F(x) + C

Ở đây, F(x) là nguyên hàm của ln(x), C là hằng số của tích phân (hằng số cộng) do quy tắc của nguyên hàm. Điều quan trọng là bạn phải biết cách tích phân để tìm được nguyên hàm của ln(x).

Bảng công thức nguyên hàm của ln(x)

Dưới đây là bảng công thức nguyên hàm In x và một số nguyên hàm cơ bản thường gặp.

Cách tính nguyên hàm của ln x

Để tính nguyên hàm của hàm số ln(x), các em hãy sử dụng quy tắc tích phân cơ bản.

∫ln(x)dx

Bước 1: Sử dụng tích phân bằng phép chia:

∫ln(x)dx = ∫1 * ln(x)dx

Bước 2: Áp dụng tích phân từng phần:

∫ln(x)dx = ∫ln(x) * 1dx

Bước 3: Sử dụng quy tắc tích phân dựa trên công thức nguyên hàm của ln(u):

∫ln(u)du = u * (ln(u) – 1) + C

Ứng dụng công thức này, ta có:

∫ln(x)dx = x * (ln(x) – 1) + C

Ví dụ minh hoạ

Tìm nguyên hàm của hàm số sau: B = x²lnxdx

Cách giải:

B=∫x²lnxdx = ∫lnxd(x³/3)

= (x³/3)lnx – ∫(x³/3).d(lnx)

= (x³/3)lnx – ∫(x³/3)*dx/3 = (x³/3)lnx – x³/9 + C

Ví dụ 2: Tính nguyên hàm ln x chứa phân thức

Ví dụ 3: Tính nguyên hàm ln x chứa căn thức

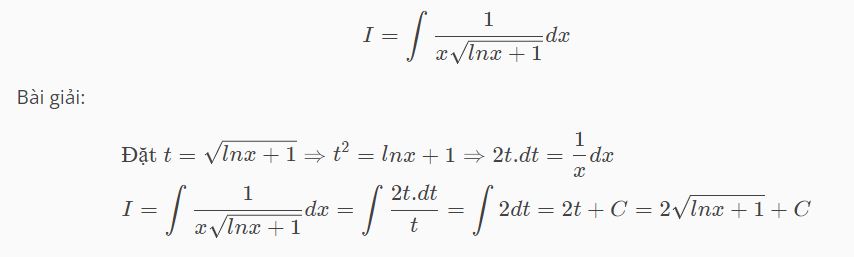
Những ứng dụng trong đời sống của ln x

Nguyên hàm của hàm lnx có ý nghĩa quan trọng trong toán học và có nhiều ứng dụng trong lĩnh vực y học. Hàm lnx đối với x là số dương là một hàm số tự nhiên. Nguyên hàm của lnx được ký hiệu là ∫lnx dx và để tính nó, ta sử dụng phương pháp tích phân. Kết quả của nguyên hàm lnx là xlnx – x + C, trong đó C là hằng số tích phân và x là biến số.

Trong lĩnh vực y học, nguyên hàm của lnx có nhiều ứng dụng quan trọng. Một trong những ứng dụng quan trọng nhất là trong việc tính toán diện tích dưới đường cong của đồ thị. Ví dụ, nó có thể được sử dụng để tính diện tích dưới đường cong của biểu đồ huyết áp, nồng độ dược phẩm trong huyết tương hoặc nồng độ hormone trong cơ thể.

Ngoài ra, nguyên hàm của lnx cũng được sử dụng để tính toán các chỉ số sinh học quan trọng như tốc độ trao đổi chất, tỷ lệ tiêu thụ năng lượng hoặc tốc độ truyền dẫn thông tin trong hệ thống thần kinh. Những tính toán này giúp chúng ta hiểu rõ hơn về các quá trình sinh lý trong cơ thể con người và đóng vai trò quan trọng trong việc chẩn đoán và điều trị các bệnh lý.

Tóm lại, nguyên hàm của lnx có ý nghĩa quan trọng trong toán học và có nhiều ứng dụng quan trọng trong lĩnh vực y học. Việc tính toán nguyên hàm này giúp chúng ta mô tả và hiểu rõ hơn về các quá trình sinh lý trong cơ thể con người và đóng vai trò quan trọng trong việc chẩn đoán và điều trị các bệnh lý.

Thông qua bài viết này, chúng tôi đã cung cấp tổng hợp kiến thức về hàm logarit tự nhiên ln(x), cách tính nguyên hàm của nó, và các ví dụ cụ thể về dạng bài tập liên quan. Chúng tôi khuyến nghị các bạn tham khảo và áp dụng kiến thức này thường xuyên để cải thiện kỹ năng tính toán.

Xem thêm: