Cấp số cộng là kiến thức quan trọng nằm trong chương trình Toán học THPT. Đây cũng là kiến thức các bạn học sinh phải nắm chắc để giải đề toán và đạt điểm cao. Cùng chúng tôi ôn lại kiến thức cơ bản về cấp số cộng, công thức cấp số cộng và bài tập minh hoạ qua nội dung dưới đây nhé.

Cấp số cộng là gì?
Cấp số cộng là khái niệm chỉ một dãy số hữu hạn hoặc vô hạn trong toán học. Trong đó, kể từ số hạng thứ 2 trở đi, mỗi số hạng đều là tổng của số hạng đứng trước nó và một số d cố định khác 0.
Công thức cấp số cộng như sau:
Với mọi n thuộc N*, Un+ 1= Un+ d
Trong đó:
- d là công sai khác 0, cố định.
- Un+ 1- Un= d với mọi n thuộc N* ( d là hằng số, Un+ 1; Un là hai số liên tiếp trong dãy cấp số cộng).
- Hiệu số Un+ 1- Un sẽ phụ thuộc vào n thì không thể là cấp số cộng.
Tính chất của công thức cấp số cộng
Nếu Un là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng đều là trung bình cộng của số đứng kế bên nó. Trừ số hạng cuối trong cấp số cộng hữu hạn. Nghĩa là Uk= ( U(k+ 1)+ U( k-1))/2 .
Tổng hợp các dạng công thức cấp số cộng
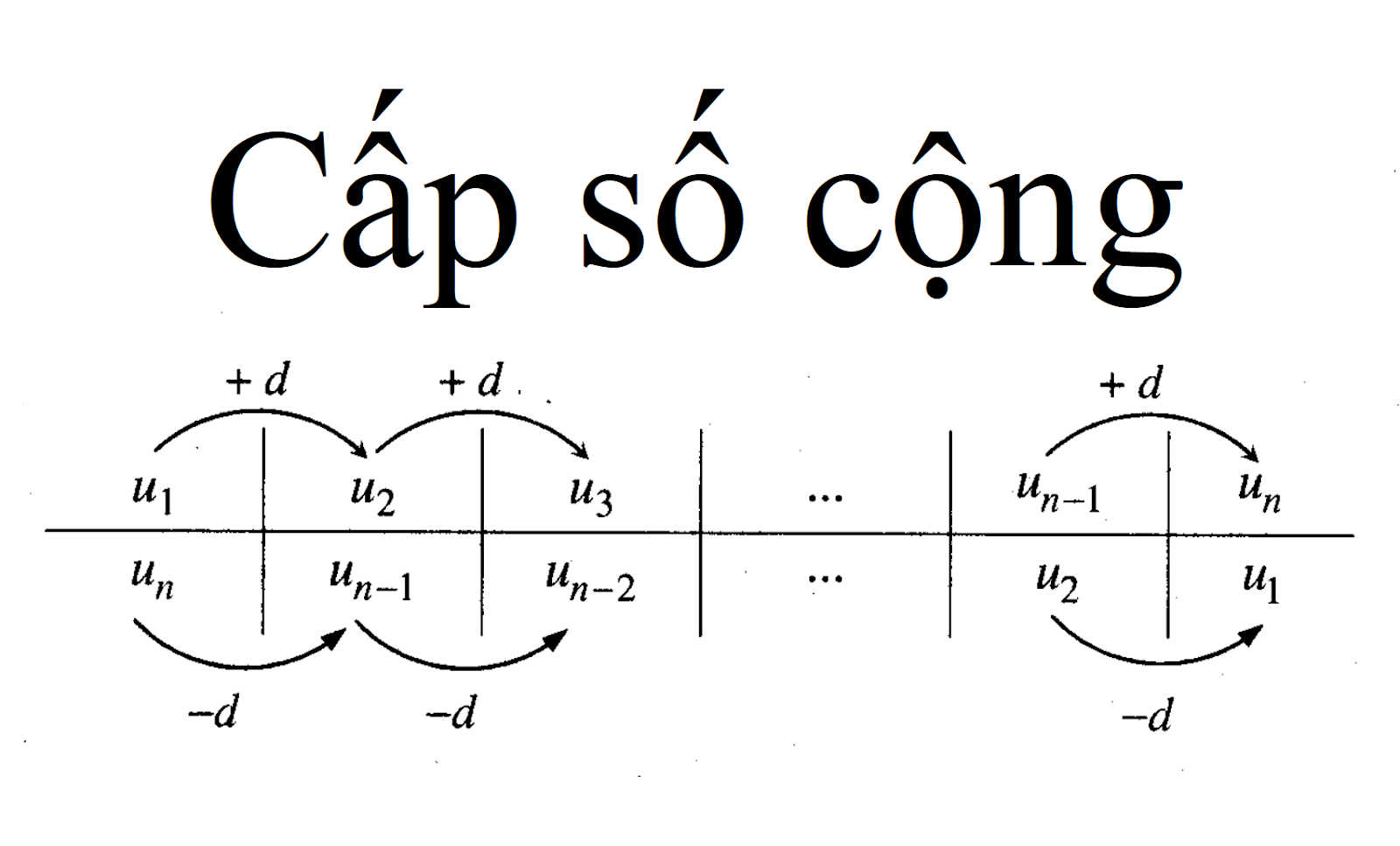
Biểu đồ các công thức cấp số cộng thường gặp
Trong chương trình Toán học đại số THPT, bạn được học rất nhiều về công thức cấp số cộng. Vì vậy, dưới đây chúng tôi sẽ tổng hợp những dạng công thức cơ bản nhất:
- Công thức CSC theo định nghĩa chung ta có: Un= Un- 1+ d ( trong đó d phải lớn hơn hoặc bằng 2).
- Công thức tìm số hạng tổng quát CSC: Un= U1 + ( n-1)d
- Công thức CSC thông qua hai số liền kề ta có: Un-1 + Un+ 1= 2Un
- Công thức cấp số liên hệ giữa hai số bất kỳ trong dãy cấp số cộng: Un= Um + ( n- m)d.
Các bài tập về công thức cấp số cộng bạn nên biết
Kiến thức về cấp số cộng được áp dụng rất nhiều trong các bài toán ở các bộ đề khác nhau. Nhằm giúp giải đề hiệu quả, đạt điểm cao, dưới đây là một vài bài tập về công thức CSC cùng hướng dẫn lời giải để bạn luyện tập:
Bài 1- Đề thi khảo sát lần 2 năm 2020 cho học sinh THPT
Đề bài cho cấp số cộng Un với U1= 3, U2= 9. Tính công sai của CSC đã cho.
Hướng dẫn giải đề:
Dựa vào khái niệm cấp số cộng ta có số hạng tổng quát Un= U1+ ( n-1)d ( U1 là số hạng đầu; d là công sai).
=> U2= U1+ d; từ đó ta có: 9= 3+ d => d= 9-3 = 6.
Vậy công sai của cấp số cộng đã cho bằng 6.
Bài tập cấp số cộng dạng 2
Cho cấp số cộng với U1= -3; U6= 27. Tìm công sai d?
Giải đề:
Đề bài cho U6= 27, U1 = -3; Khi đó ta có:
Dựa theo công thức CSC như sau: U1+ 5d= 27
=> -3 + 5d= 27 => 5d= 27- ( -3) => 5d= 30 => d= 30/5= 6.
Vậy công sai d cần tìm bằng 6.
Đề số 3- Đề thi thử chuyên Vinh- Nghệ An.
Đề bài: Tìm 4 số hạng liên tiếp của CSC. Biết tổng của 4 số đó bằng 20 và tổng các bình phương bằng 120.
Lời giải:
Theo đề bài, giả sử 4 số hạng liên tiếp đó là a+ x; a- 3x, a- x; a+ 3x; công sai d= 2x. Khi đó ta có:
( a- 3x) + ( a-x) + ( a+ x) + ( a + 3x) = 20 => 4a= 20 => a= 5
Và ( a- 3x)^2 + ( a-x)^2 + ( a+ x)^2 + ( a + 3x)^2= 120 => 4a^2 + 20x^2= 120=> x= ± 1.
Suy ra: 4 số liên tiếp trong dãy cấp số cộng lần lượt là 2, 4, 6, 8.
Dạng bài CSC thứ 4
Đề bài: Xác định a để 3 số 1+ 3a; a^2+ 5 và 1-a theo thứ tự lập thành một dãy cấp số cộng.
Lời giải:
Ta có 3 số đã cho gồm: 1+ 3a, a^2+ 5, 1-a theo thứ tự dãy cấp số cộng ⇔ a^2+ 5 – ( 1+ 3a)= 1- a – ( a^2+ 5)
Suy ra: a^2- 3a+ 4 = -a^2 – a- 4 => a^2- a+ 4= 0
Vậy phương trình vô nghiệm.

Giải bài toán về CSC
Qua nội dung bài viết, chắc hẳn bạn đã hiểu hơn về công thức cấp số cộng cũng như biết cách giải một số đề toán. Mong rằng bạn sẽ vận dụng tốt kiến thức cấp số cộng trong mọi kỳ thi của bản thân.