Nếu các em đã quen thuộc với bài tập tính luỹ thừa thì logarit là dạng ngược lại của nó, logarit là một trong những dạng bài tập thường xuyên xuất hiện trong các kỳ thi THPT Quốc Gia. Hãy cùng imo2007.edu.vn tổng hợp lại tất cả công thức logarit để các em nắm lại nhé.
Logarit là gì?
Logarit là một khái niệm trong toán học, được sử dụng để giải quyết các phép tính liên quan đến lũy thừa và bài toán liên quan đến mức độ tăng dần của các dãy số. Logarit của một số x theo cơ số b (thường là số dương khác 1) được ký hiệu là log_b(x) và thường đọc là “logarit cơ số b của x”.
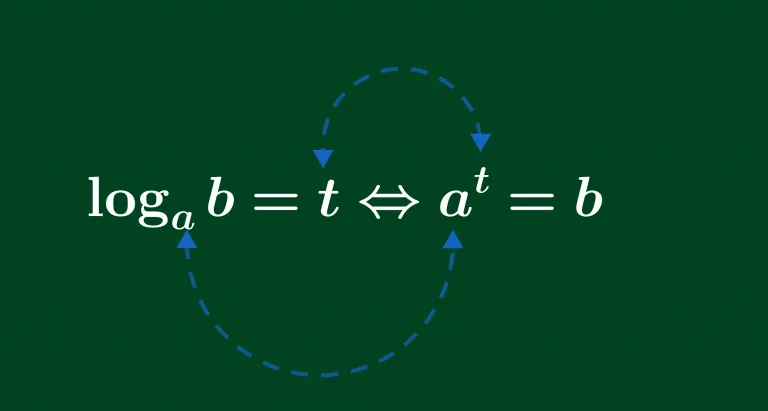
Cụ thể, nếu b^y = x, thì ta nói y là logarit cơ số b của x, hay y = log_b(x). Trong đó:
- b là cơ số của logarit.
- x là số mà chúng ta muốn tính logarit của.
- y là kết quả logarit.
Ví dụ:
Nếu b = 10 và x = 100, thì log_10(100) = 2, vì 10^2 = 100.
Nếu b = 2 và x = 8, thì log_2(8) = 3, vì 2^3 = 8.
Tổng hợp công thức logarit đầy đủ


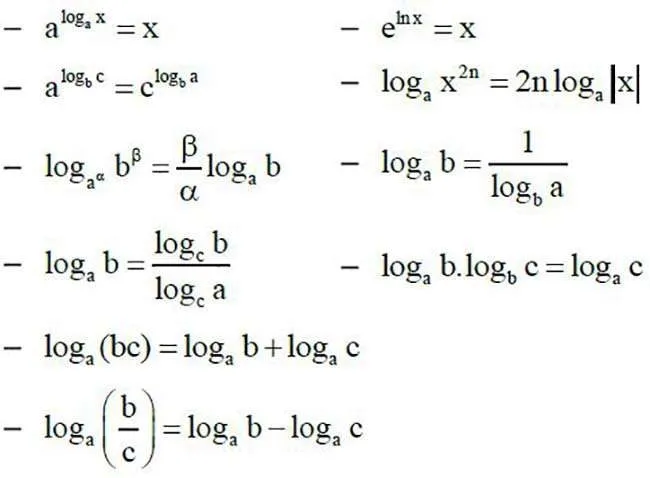
Hệ thống lại công thức luỹ thừa
Để học tốt công thức logarit thì các em cũng cần nắm vững các công thức về luỹ thừa


Công thức Logarit và các phép toán

Công thức phép đổi cơ số

Công thức tính đạo hàm Logarit

Những điều thú vị về logarit
Lịch sử logarit
Khái niệm logarit được giới thiệu vào thế kỷ 17 bởi nhà toán học người Scotland John Napier. Ông đã phát triển bảng logarit đầu tiên, giúp nhân và chia trở nên dễ dàng hơn bằng việc thực hiện phép cộng và trừ trên các số logarit thay vì phép nhân và chia trên các số gốc.
Sự tương quan với phép cấp số nhân và cấp số mũ
Logarit và lũy thừa có một mối quan hệ chặt chẽ. Khi bạn tính logarit cơ số b của một số, bạn đang tìm số mũ bao nhiêu để có được số đó. Điều này liên kết với khái niệm của phép cấp số nhân và cấp số mũ.
Thang logarit
Các số logarit của các cơ số khác nhau tạo thành một loạt gọi là “thang logarit”. Điều này thể hiện mối quan hệ giữa các cơ số logarit khác nhau. Thang logarit thường được sử dụng để giúp thực hiện tính toán logarit nhanh chóng.
Ứng dụng trong khoa học và kỹ thuật
Logarit có nhiều ứng dụng quan trọng trong các lĩnh vực như toán học, khoa học, kỹ thuật, thống kê, và tính toán phức tạp. Chẳng hạn, trong ngành công nghệ thông tin, logarit được sử dụng để đo độ phức tạp của thuật toán và phân tích hiệu suất.
Chuyển đổi hệ số logarithmic (dB)
Trong công nghệ và điện tử, đơn vị đo dB (decibel) được sử dụng để biểu thị mức độ tăng giảm trong các tín hiệu như âm thanh và sóng điện từ. Đơn vị này dựa trên logarithm với cơ số 10 và được sử dụng để thể hiện mức độ khác biệt trong cường độ của các tín hiệu.
Phân phối logarithmic
Trong nhiều khía cạnh của tự nhiên và xã hội, sự phân phối logarithmic xuất hiện thường xuyên. Một ví dụ phổ biến là phân phối định giá của sản phẩm, trong đó có một số ít các sản phẩm có giá trị cao và nhiều sản phẩm có giá trị thấp.
Logarit tự nhiên (ln)
Logarit tự nhiên là logarit theo cơ số e, một hằng số rất quan trọng trong toán học và các lĩnh vực khoa học khác. Logarit tự nhiên thường được ký hiệu là ln(x).
Như vậy, các em vừa hệ thống lại công thức logarit rất quan trọng của chương trình lớp 12, chúc các em học thật tốt.
