Phép tịnh tiến là một trong những dạng toán lớp 11 phổ biến, trong bài viết dưới đây, cùng imo2007 tìm hiểu công thức phép tịnh tiến chi tiết và ví dụ minh họa nhé.
Phép tịnh tiến là gì?
Phép tịnh tiến là một phép biến hình trong hình học không gian, trong đó các điểm trong không gian được dịch chuyển song song theo một hướng và khoảng cách xác định. Trên mặt phẳng, phép tịnh tiến biến đổi mỗi điểm thành một điểm mới bằng cách dịch chuyển nó theo một vectơ với hướng và độ dài xác định.
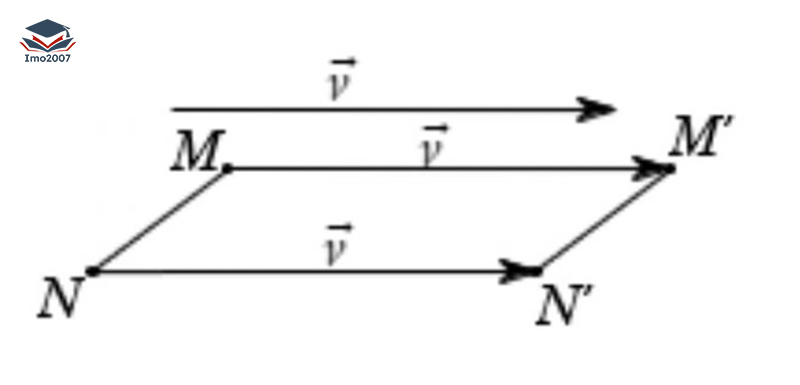
Công thức phép tịnh tiến
Công thức phép tịnh tiến trên mặt phẳng cho vectơ v = (a, b) như sau:
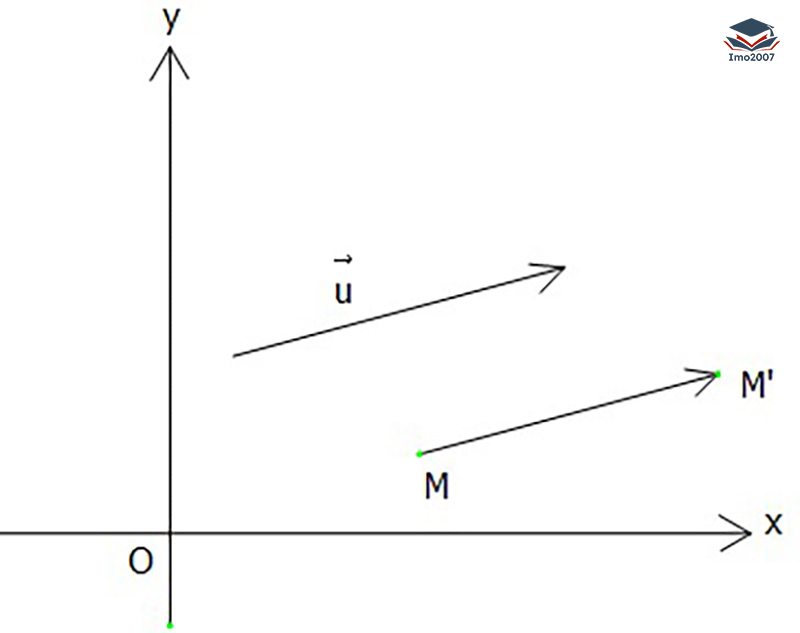
Đối với mỗi điểm M(x, y), ta có điểm M’ mới là ảnh của M qua phép tịnh tiến theo vectơ v.
Tọa độ của điểm M’ được tính bằng cách thêm giá trị của vectơ tịnh tiến v vào tọa độ của điểm M: x’ = x + a và y’ = y + b.
Phép tịnh tiến được sử dụng rộng rãi trong hình học và các lĩnh vực khác, như đồ họa máy tính, xử lý ảnh, và công nghệ điện tử. Nó có tính chất bảo toàn một số đặc tính quan trọng, chẳng hạn như khoảng cách giữa các điểm và các đặc tính hình học của các hình, giúp đơn giản hóa tính toán và mô phỏng trong các ứng dụng thực tế.
Phép tịnh tiến theo vectơ – không được gọi là phép đồng nhất. (Biến mỗi điểm thành chính nó)
Tính chất của phép tịnh tiến
– Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
– Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
– Biến một vecto thành 1 vectơ bằng nó.
– Biến tam giác thành tam giác bằng nó.
– Biến một góc thành một góc bằng nó.
– Biến đường tròn thành đường tròn có cùng bán kính.
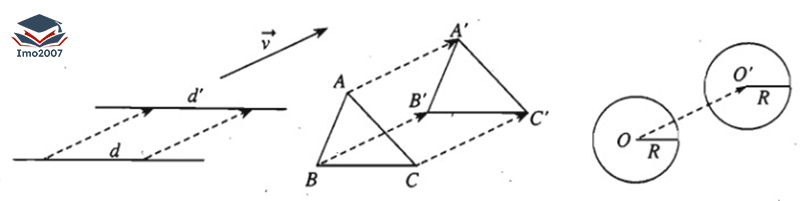
Ví dụ minh họa
Sau khi đã biết được công thức phép tịnh tiến, chúng ta cùng đi đến những ví dụ minh họa sau để nắm rõ hơn nhé.
Ví dụ 1:
Trên mặt phẳng Oxy, ta có điểm A(2, 3). Áp dụng phép tịnh tiến theo vectơ v = (4, -1), hãy xác định điểm A’ là ảnh của A sau phép tịnh tiến.
Theo công thức phép tịnh tiến, ta có:
x’ = x + a
y’ = y + b
Áp dụng vào ví dụ, với điểm A(2, 3) và vectơ tịnh tiến v = (4, -1), ta có:
x’ = 2 + 4 = 6
y’ = 3 – 1 = 2
Vậy điểm A’ có tọa độ là A'(6, 2) là ảnh của điểm A(2, 3) sau phép tịnh tiến theo vectơ v = (4, -1).
Ví dụ 2:
Trên mặt phẳng Oxy, cho đường tròn (C) có tâm I(2, -1) và bán kính R = 3. Áp dụng phép tịnh tiến theo vectơ v = (-1, 2), hãy xác định đường tròn (C’) là ảnh của đường tròn (C) sau phép tịnh tiến.
Để xác định đường tròn (C’) sau phép tịnh tiến, ta cần tìm tọa độ của tâm I’ và bán kính R’ của đường tròn (C’).
Theo công thức phép tịnh tiến, tọa độ tâm I’ của đường tròn (C’) được tính bằng cách thêm giá trị của vectơ tịnh tiến v vào tọa độ của tâm I:
x_I’ = x_I + a = 2 – 1 = 1
y_I’ = y_I + b = -1 + 2 = 1
Vậy tâm I’ của đường tròn (C’) có tọa độ là I'(1, 1).
Bán kính R’ của đường tròn (C’) giữ nguyên và bằng bán kính R của đường tròn (C).
Vậy đường tròn (C’) có tâm I'(1, 1) và bán kính R’ = 3 là ảnh của đường tròn (C) sau phép tịnh tiến theo vectơ v = (-1, 2).
Bài tập tự luyện ở nhà
Câu 1. Trong mặt phẳng Oxy, cho điểm M(0; 1). Ảnh của điểm M qua phép tịnh tiến theo vectơ u=( 2 ; 3 ) là điểm nào?
A. M'(2; 3)
B. M'(1; 3)
C. M'(1; 1)
D. M'(-1; -1)
Câu 2. Trong mặt phẳng Oxy, cho đường thẳng d: x – 2y + 2 = 0. Ảnh của đường thẳng d qua phép tịnh tiến theo
→
u = (2 ; 3)
có phương trình là:
A. x + 2y + 2 = 0
B. x – 2y + 6 = 0
C. 2x – y + 2 = 0
D. 2x + y +2 = 0
Câu 3. Trong mặt phẳng Oxy, cho đường tròn (C): x² + y² – 2x + 4y – 4 = 0. Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ u = ( 1 ; 1 )
là đường tròn có phương trình:
A. (x – 2)² + (y + 1)² = 16
B. (x + 2)² + (y – 1)² = 9
C. (x – 2)² + (y + 1)² = 9
D. (x + 2)² + (y + 1)² = 9
Đáp án: 1B, 2B, 3C
Trên đây là bài viết về công thức phép tịnh tiến mà các em sẽ được học trong chương trình toán lớp 11, các em hãy tự luyện thêm các bài tập để nắm vững về các dạng toán của phép biến hình này nhé. Chúc các em học tốt.
Xem thêm: Công thức phép quay trong toán học