Số phức là một phần kiến thức quan trọng trong toán học đại số lớp 12. Đây cũng là phần kiến thức khó nhất dành cho học sinh THPT. Vậy những kiến thức cơ bản về tập số này là gì? Hãy cùng theo dõi bài viết dưới đây để hiểu và nắm được vài bài tập cơ bản về dạng số này nhé.
Số phức là gì?

Khái niệm số phức là gì
Nhiều bạn thắc mắc số phức là gì? Thì số phức trong toán học đại số sẽ có dạng z= a+ bi. Trong đó, a và b là các số nguyên, a là phần thực, b là phần ảo của số z. Còn i được gọi là đơn vị ảo, quy ước i^2= -1. Trường hợp z là số thực thì b phần ảo sẽ bằng 0 và ngược lại, z là thuần ảo thì a=0.
Ký hiệu tập hợp số phức là C.
Đối với số phức, chúng ta chỉ xét hai số có bằng nhau hay không. Với z = a + bi và z’= a’ + b’i. Điều kiện để hai số phức bằng nhau z= z’ khi a= a’ và b= b’.
Số phức được biểu diễn như thế nào
Số phức z= a+bi với a,b là số nguyên. Xét trong mặt phẳng Oxy, z được biểu diễn ở điểm M( a; b) hoặc u= ( a; b). Trong mặt phẳng Oxy, trục Ox là trục thực, Oy là trục ảo.
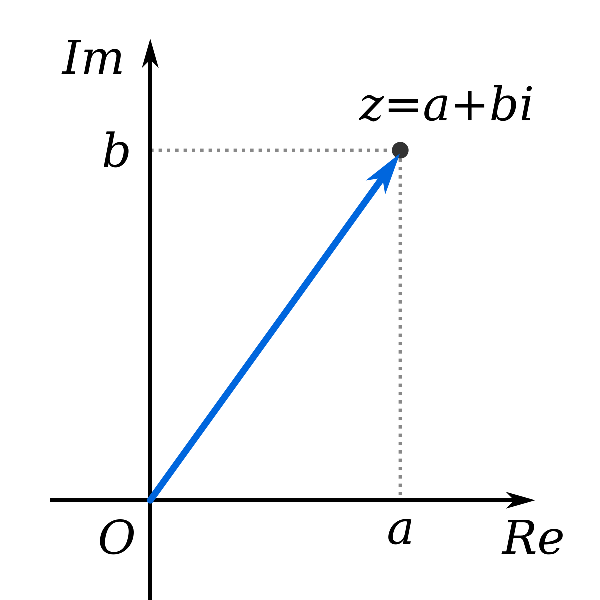
Hình biểu diễn số phức
Ứng dụng số phức trong toán hình học, lượng giác
Số phức không chỉ được áp dụng để giải các đề toán đại số. Mà nó còn được dùng trong các phép tính toán hình học, lượng giác. Theo khái niệm thì i là sự quay và chuyển hướng 90 độ nên số phức có vai trò rất quan trọng trong giải các dạng bài tập hình học. Và để giải các dạng bài tập hình học, bạn chỉ cần vận dụng chính xác kiến thức về số phức với bài toán hình phẳng hoặc tính công thức lượng giác.
Ngoài ra, số phức còn được áp dụng để giải các bài tập phân tích đa thức ra thừa số hay các bài tập về tích phân… Bên cạnh đó, kiến thức số phức còn được dùng để tính toán các ví dụ, bài tập trong bộ môn vật lý.
Các dạng bài tập về số phức trong toán học đại số
Giải các dạng bài tập về số phức nhiều sẽ rất tốt cho hành trình thi cử của học sinh. Dưới đây là một số dạng bài tập đơn giản về tập hợp số z để bạn tham khảo, giải đề:
Dạng bài 1: Tìm số thực x, y sao cho các đẳng thức sau là đúng
- 5x+y + 5xi= 2y- 1 + ( x-y)i
- ( -3x + 2y)i + ( 2x- 3y + 1)= ( 2x+ 6y- 3)+ ( 6x-2y)i
Hướng dẫn giải:
- Xem xét mỗi vế là một số phức. Như vậy, áp dụng điều kiện để 2 số phức bằng nhau ta có:
5x+ y= 2y- 1; 5x= x- y => x= -1/7; y= 4/7.
- Phần này giải tương tự phần a. Bạn chỉ cần xem xét phần thực bằng phần thực, phần ảo bằng phần ảo để tính toán là ra. Cụ thể:
2x- 3y+ 1= 2x+6y- 3; ( -3x+ 2y)= 6x- 2y
Dạng bài 2: Tìm số phức khi biết: |z| = 5; z= z
Hướng dẫn giải:
Theo khái niệm ta có, z= a+ bi, => z= a- bi. Khi đó, a^2+ b^2= 52; a= a; b= -b ( bởi z= z).
=> b= 0 và a= 5.
Vậy số phức z thỏa mãn đề bài là z= 5 và z= -5.
Dạng bài 3: Tìm số phức theo căn bậc hai và phương trình
Cho số z= a+ bi, số phức w = x+ yi là căn bậc hai của z nếu w2= z.
Hay nói cách khác, ( x+y)^2 = a+ bi.
=> Suy ra x2- y2 + 2xyi= a+ bi
=> x2- y2= a và 2xy= b.
Đề bài: Tìm giá trị m để phương trình z+ mz+ i= 0. Có hai nghiệm z1, z2 thỏa đẳng thức z12+ z2 2= -4i
Hướng dẫn giải:
Theo khái niệm thì phương trình căn bậc 2 có hệ thức vi- et. Từ đó ta có: z1+ z2= -m, z1z2= i.
Ta có: z12+ z2 2= -4i => ( z1+ z2)^2 – 2z1z2 = -4i
=> m2 sẽ bằng -2i.
Đến đây, bài toán đã quy về tìm căn bậc 2 của số phức. Ta áp dụng công thức m= a+ bi được:
a^2+ b^2= 0, 2ab= -2i => ( a, b)= 1, -1) hoặc ( a, b) bằng ( -1, 1). Như vậy, có hai giá trị m để thỏa mãn đề bài.

Các dạng bài tập minh hoạ
Trên đây là tổng hợp kiến thức cơ bản và một số bài tập về số phức chúng tôi chia sẻ để bạn tham khảo. Mong rằng những kiến thức này sẽ giúp bạn vận dụng tốt nhất vào việc giải đề thi hiệu quả.