Phương trình tham số và những kiến thức trọng tâm cần biết

Phương trình tham số là kiến thức trọng tâm mà học sinh nào cũng phải nắm chắc ngay từ đầu cấp THPT. Hiểu và nắm chắc lượng kiến thức về dạng phương trình này sẽ giúp bạn dễ dàng giải các bài tập hình học cũng như các đề toán nâng cao. Nhằm giúp bạn củng cố kiến thức về dạng phương trình t, chúng tôi đã tổng hợp đầy đủ qua nội dung bài viết dưới đây. Mời bạn cùng tham khảo và ôn tập nhé. 

Khái niệm phương trình tham số là gì

Phương trình các tham số 

Phương trình tham số được xác định bởi hệ các hàm số của một hoặc nhiều biến độc lập gọi là tham số. Tham số trong phương trình được ký hiệu là t và được sử dụng để biểu diễn các toạ độ của các điểm thuộc hình học. Ví dụ như đường cong hoặc bề mặt… Các đối tượng này được biểu diễn theo tham số hoặc tham số hoá. 

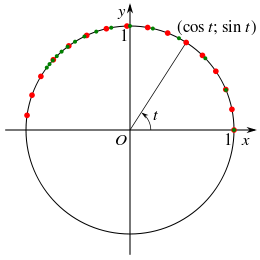
Ví dụ minh hoạ: Phương trình biểu diễn bằng tham số của đường tròn, với ( t) là tham số có dạng như sau: 

x= cos t

y= sin t

Phương trình tham số biểu diễn đường thẳng trong mặt phẳng Oxy

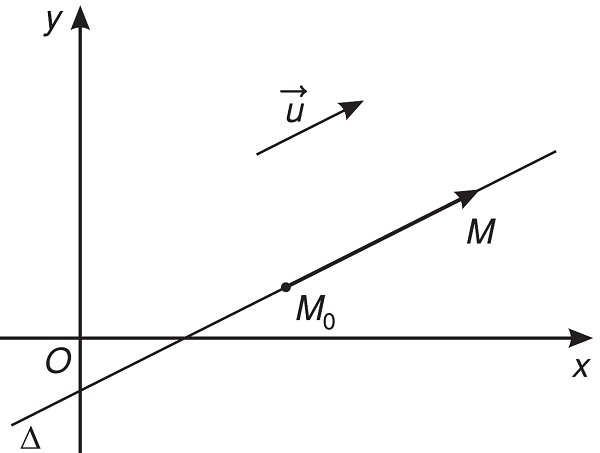
Phương trình các tham số t của đường thẳng đi qua điểm A( x0; y0) nhận →u( a,b) làm vectơ chỉ phương. Khi đó ta có phương trình sau:

d: x= x0 + at và y= y0+ at

Với điều kiện, a^2 + b^2 ≠ 0 được gọi là phương trình tham số của đường thẳng d, với t là tham số. 

Tổng hợp các dạng phương trình tham số thường gặp

Phương trình ( t) được ứng dụng rộng rãi trong bộ môn toán học cũng như đời sống. Dưới đây là những dạng phương trình tham số thường gặp nhất để bạn tham khảo: 

Ví dụ minh hoạ về phương trình tham số

Để hiểu và giải được nhiều bài tập hơn, những ví dụ dưới đây chắc chắn sẽ hữu ích dành cho bạn: 

Ví dụ 1: Viết phương trình tham số với 3 điểm A ( -2; 1), B( -1; 5), C ( -2; -3). 

Yêu cầu: 

1. Viết phương trình cho tham số AB, AC.
2. Viết phương trình cho tham số đường trung trực cạnh BC.
3. Viết phương trình đường thẳng song song với AB và đi qua trung điểm BC. 

Hướng dẫn bài giải: 

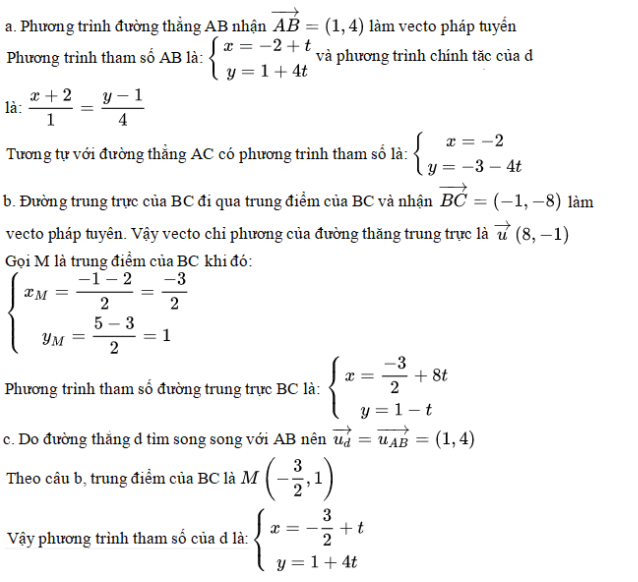
Ví dụ 2: Viết phương trình đường thẳng

Cho đường thẳng y= ax + b biết rằng: 

1. Đường thẳng y = ax + b đi qua 2 điểm A( -3; 2), B( 5; -4). Tính diện tích tam giác được tạo bởi 2 trục toạ độ và đường thẳng đó. 
2. Đường thẳng đi qua A ( 3; 1) song song với đường thẳng y= -2x + m- 1

Hướng dẫn giải đề: 

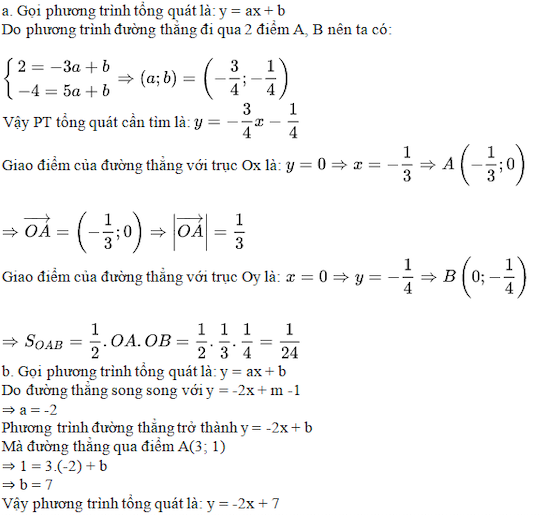
Một số bài tập tự luyện dành cho bạn

Áp dụng những kiến thức và cách tính phương trình tham số, bạn có thể thực hành giải các dạng bài tập khác nhau. Dưới đây là một vài bài tập giúp bạn tự luyện đề hiệu quả: 

Bài 1: Đề bài cho tam giác ABC với A ( -2; 1), B ( -1; 5), C ( 2; 3). Viết phương trình tham số cho:

1. Các cạnh AB, BC, AC. 
2. Viết phương trình cho đường trung tuyến AM, CP với M, P là trung điểm của cạnh BC và AB. 
3. Viết phương trình cho đường cao AH
4. Viết phương trình cho đường thẳng đi qua A, song song với cạnh BC. 
5. Viết phương trình đường thẳng đi qua B, vuông góc với y= 2x – 3. 

Dạng bài tự luyện 2: Viết phương trình tham số, phương trình chính tắc trong các trường hợp:

1. Đường thẳng d đi qua 2 điểm A, B. Trong đó, A ( -2; 0) , B ( 1; 3). 
2. Đường thẳng d đi qua M( 3; -2) song song đường thẳng 2x+ 5y-4= 0.
3. Hệ số góc k của đường thẳng d bằng 1 và đi qua điểm D ( -1; 1). 

Bài tập 3: Đề bài cho hai đường thẳng ( d1) và ( d2) như sau: 

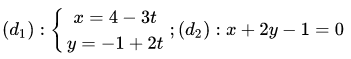
1. Xác định toạ độ giao điểm A của hai đường thẳng d1 và d2. 
2. Viết phương trình tham số, phương trình tổng quát của đường thẳng đi qua A và vuông góc d1, song song với d2. 

Cách tính phương trình ( t)

Vậy là nội dung bài viết trên đây chúng tôi đã giới thiệu đến bạn lý thuyết về phương trình tham số. Cùng với cách tính phương trình trong toán hình học. Hy vọng những chia sẻ từ bài viết giúp bạn nắm vững hơn phần kiến thức trọng tâm này. Hãy theo dõi website của chúng tôi để không bỏ lỡ kiến thức toán học nào mới và hay nhất nhé.