Công thức tính diện tích tam giác là một khái niệm quan trọng và cơ bản trong hình học. Tam giác, với những đường cạnh và góc khác nhau, tạo nên một hình dạng độc đáo và hấp dẫn. Việc tính toán diện tích của một tam giác không chỉ giúp chúng ta hiểu rõ hơn về hình dạng này, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Trong bài viết này, imo2007 sẽ chia sẻ đến các em công thức tính diện tích tam giác và cách áp dụng nó để giải quyết các bài toán liên quan.
Thế nào là một hình tam giác?
Hình tam giác là một hình học ba cạnh được hình thành bởi ba đoạn thẳng, gọi là các cạnh, và ba đỉnh nằm ở giao điểm của các cạnh. Tam giác có tổng cộng ba cạnh, ba góc và ba đỉnh. Các cạnh của tam giác có thể có độ dài và hướng khác nhau, tạo nên các loại tam giác khác nhau, chẳng hạn như tam giác đều, tam giác vuông, tam giác cân và tam giác tù.
Tam giác được đặc trưng bởi các thuộc tính như độ dài các cạnh, góc giữa các cạnh, tỉ lệ giữa các cạnh và các góc, cùng với các định dạng đặc biệt như tam giác vuông có một góc vuông (90 độ). Các tam giác có thể được phân loại dựa trên các thuộc tính này và được sử dụng trong nhiều lĩnh vực như toán học, hình học, vật lý, xây dựng và thiết kế.

Hình tam giác có nhiều ứng dụng trong cuộc sống hàng ngày và các ngành công nghiệp. Chẳng hạn, trong xây dựng, tam giác được sử dụng để tính toán diện tích các bề mặt, xác định vị trí và hình dạng của các thành phần kiến trúc. Trong hình học và toán học, tam giác là một trong những hình dạng cơ bản và đóng vai trò quan trọng trong việc phát triển các khái niệm và công thức tính toán trong hình học Euclid và hình học không gian.
Với các đặc tính và ứng dụng đa dạng của nó, tam giác là một khía cạnh quan trọng trong nghiên cứu và ứng dụng hình học, đồng thời mang lại những hiểu biết và kỹ năng tính toán hữu ích trong cuộc sống hàng ngày.
Những dạng hình tam giác thường gặp
Trước khi đi đến công thức tính diện tích tam giác thì các em cần biết tất cả các dạng hình tam giác thường gặp để áp dụng công thức tính một cách phù hợp. Hãy xem các dạng hình tam giác có gì đặc biệt nhé:
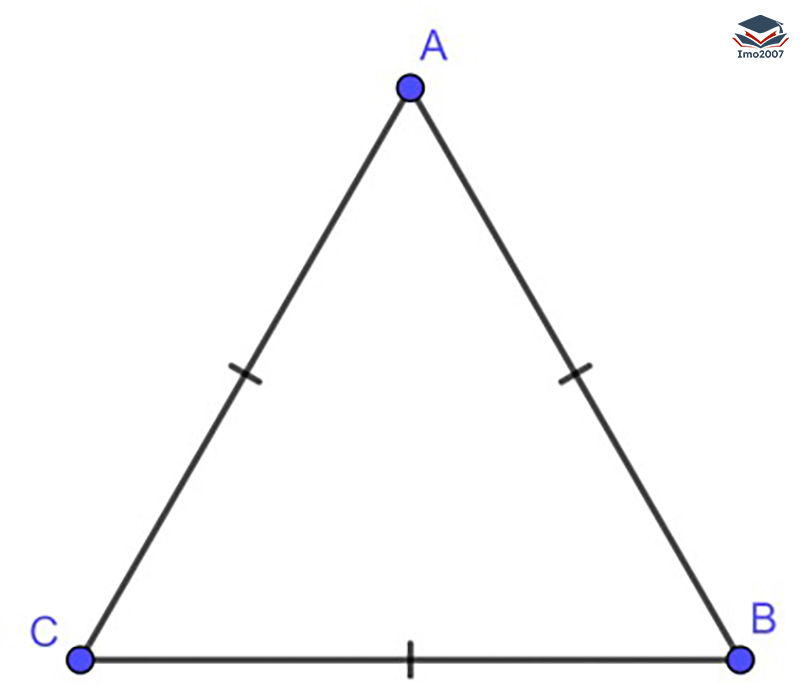
Tam giác đều: Tam giác đều là tam giác có ba cạnh và ba góc bằng nhau. Tất cả các cạnh và góc trong tam giác đều đều có giá trị như nhau.
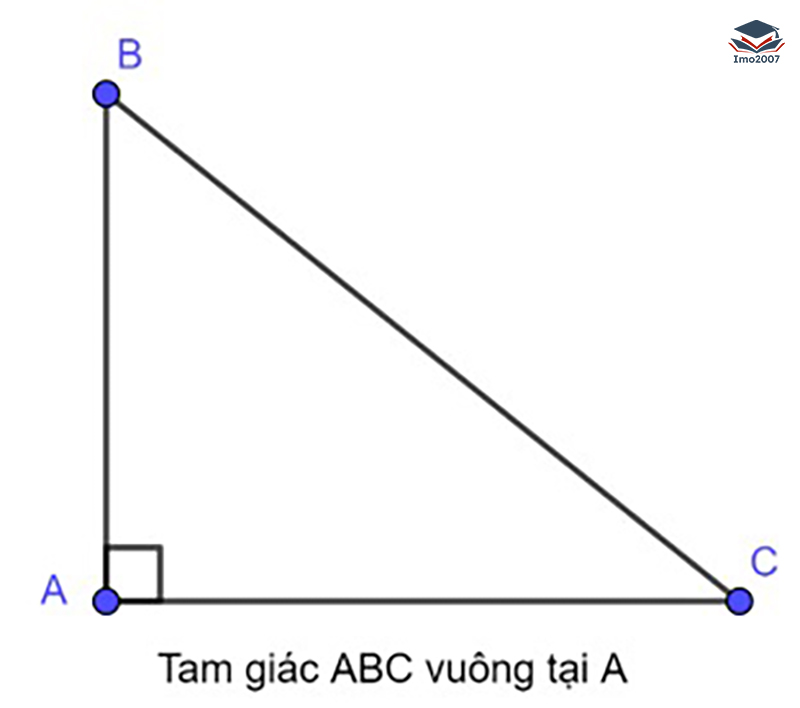
Tam giác vuông: Tam giác vuông có một góc vuông, tức là một góc có giá trị chính xác là 90 độ. Cạnh đối diện với góc vuông trong tam giác vuông được gọi là cạnh huyền, trong khi hai cạnh còn lại được gọi là cạnh góc nhọn.
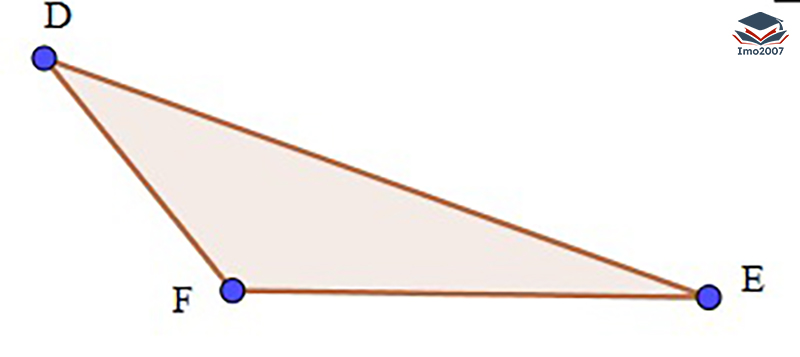
Tam giác tù: Tam giác tù có một góc lớn hơn 90 độ, được gọi là góc tù. Hai góc còn lại là góc nhọn.
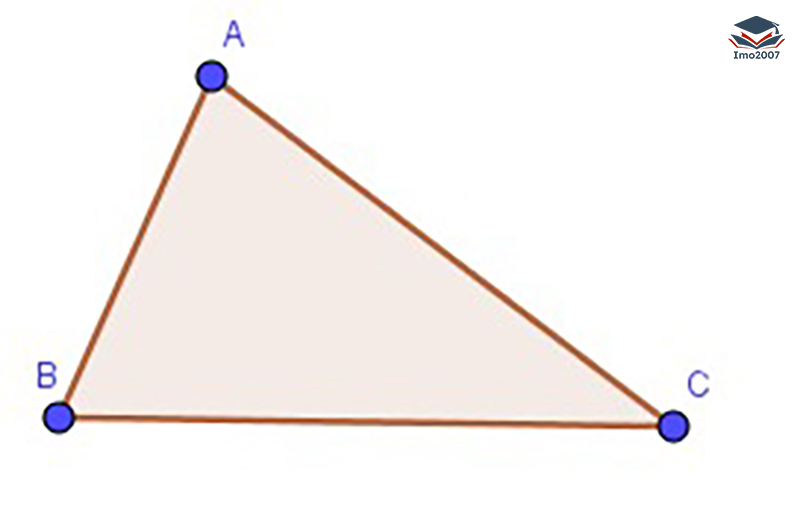
Tam giác nhọn: Tam giác nhọn có ba góc nhọn, tức là tất cả ba góc đều nhỏ hơn 90 độ.
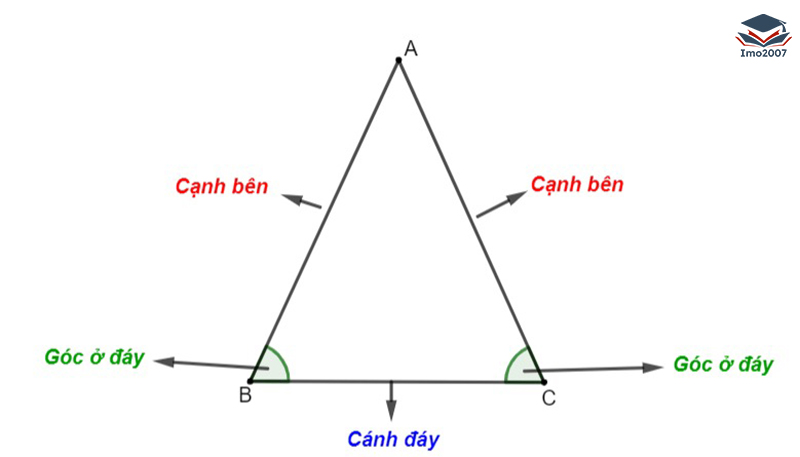
Tam giác cân: Tam giác cân có ít nhất hai cạnh bằng nhau. Điều này có nghĩa là hai góc ở đỉnh đối diện với các cạnh bằng nhau cũng bằng nhau.
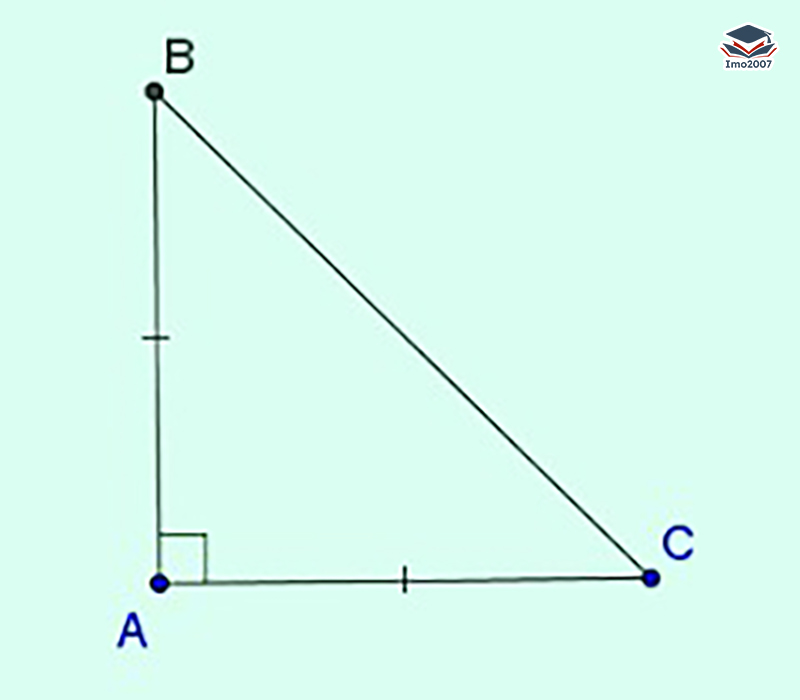
Tam giác vuông cân: Tam giác vuông cân là một tam giác có một góc vuông và hai cạnh góc nhọn bằng nhau.
Ngoài các loại tam giác trên, còn có các loại tam giác đặc biệt khác như tam giác đối xứng, tam giác Pitago, tam giác Fibonacci, tam giác Fermat, tam giác hình bàn cờ, và nhiều loại tam giác khác nữa. Mỗi loại tam giác có những đặc điểm riêng và có ứng dụng trong lĩnh vực khác nhau của toán học, hình học và các ngành công nghiệp liên quan.
Công thức tính diện tích tam giác
Cách tính diện tích tam giác thường
Công thức tính diện tích tam giác thường
S = (a x h)/2
Trong đó:
a là chiều dài đáy tam giác (đáy là một trong ba cạnh của tam giác tùy thuộc vào cách đặt của người tính)
h là chiều cao của tam giác, tương ứng với phần đáy chiếu lên (chiều cao của một tam giác được xác định là đoạn thẳng hạ từ đỉnh xuống đáy, đồng thời vuông góc với đáy của tam giác).
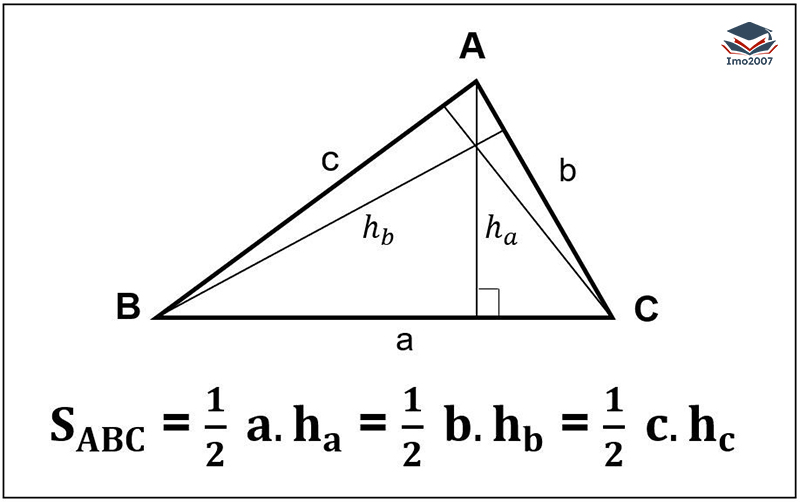
Công thức suy ra:
h = (S x 2) / a hoặc a = (S x 2) / h
Công thức tính diện tích tam giác vuông
Diện tích tam giác vuông được tính bằng: ½ tích chiều cao với chiều dài đáy.
Công thức tính diện tích hình tam giác vuông
S = ½ (a x b)
Trong đó: a, b là độ dài của hai cạnh góc vuông
Công thức tính diện tích tam giác cân
Diện tích của tam giác cân bằng tích của chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác và chiều dài đáy tam giác cân, sau đó lấy kết quả chia cho 2.
Công thức tính
S = ½ (a x h)
Trong đó:
a là độ dài của cạnh đáy
b là độ dài của hai cạnh bên
h là đường cao từ đỉnh xuống cạnh đáy
Công thức tính diện tích tam giác đều
Công thức tính diện tích hình tam giác đều (áp dụng định lý Heron)
S = a2 x (√3/4)
Trong đó: a là độ dài các cạnh
Công thức tính diện tích tam giác vuông cân
Công thức tính:
S = ½ x (a2)
Trong đó: tam giác ABC vuông cân tại A và a là độ dài hai cạnh góc vuông.
Như vậy, thông qua công thức tính diện tích hình tam giác ở các dạng thì các em đã nắm vững các kiến thức về dạng hình này để chuẩn bị thật tốt cho các kỳ thi. Chúc các em hoàn thành tốt các bài kiểm tra của mình và luôn mãi yêu môn Toán nhé.
Xem thêm: Cách tính độ dài vecto: Hướng dẫn chi tiết và ví dụ minh họa