Hình thang là một dạng hình học phổ biến trong chương trình môn Toán, cách tính chu vi hình thang, diện tích hình thang là dạng kiến thức cơ bản mà các em cần phải nắm vững vì nó xuất hiện rất nhiều trong các kỳ thi. Thậm chí còn ứng dụng rất nhiều trong đời sống hàng ngày.
Hình thang là gì?
Hình thang là một hình học có bốn cạnh, trong đó hai cạnh đối diện song song và có độ dài khác nhau. Hình thang có bốn đỉnh và bốn góc. Đáy lớn và đáy nhỏ của hình thang là hai cạnh song song và nằm ở hai phía đối diện của hình thang. Các cạnh còn lại được gọi là cạnh bên của hình thang. Tổng các góc bên trong hình thang luôn bằng 360 độ.
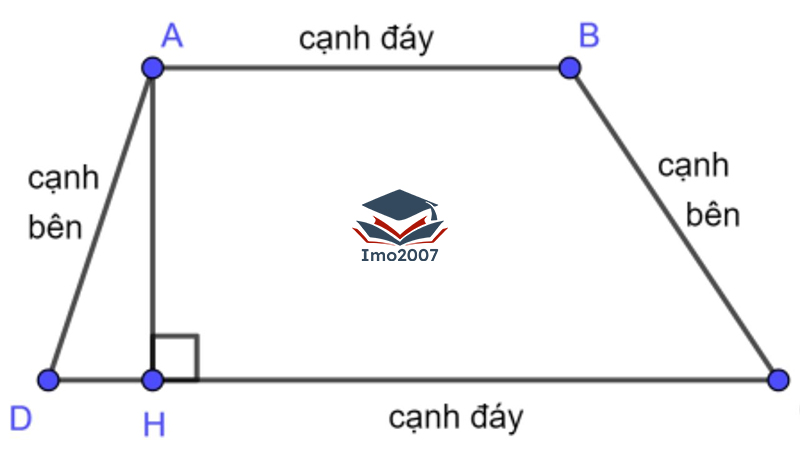
Có 3 dạng thù hình của hình thang, là hình thang thường, hình thang cân và hình thang vuông. Hình thang là một hình học phổ biến và được sử dụng trong nhiều lĩnh vực, như toán học, kiến trúc, và hình học không gian.
Cách tính chu vi hình thang
Để tính chu vi hình thang, ta cần biết độ dài hai đáy và độ dài hai cạnh bên của hình thang. Gọi độ dài hai đáy lần lượt là a và b, và độ dài hai cạnh bên là c và d.
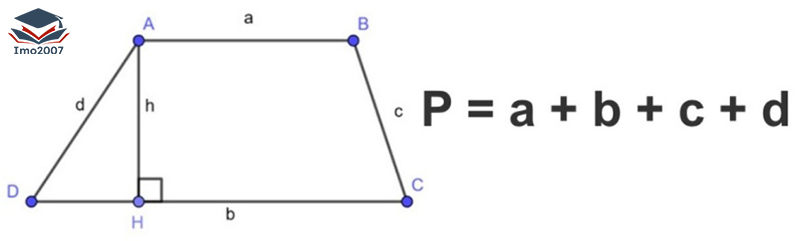
Công thức tính chu vi hình thang là:
Chu vi = a + b + c + d
Ví dụ, nếu ta có một hình thang với đáy lớn a = 10 cm, đáy nhỏ b = 6 cm, cạnh bên c = 7 cm và cạnh bên d = 9 cm, ta có thể tính chu vi như sau:
Chu vi = 10 cm + 6 cm + 7 cm + 9 cm = 32 cm
Vậy chu vi của hình thang trong ví dụ trên là 32 cm.
Công thức tính chu vi hình thang cân
Từ cách tính chu vi hình thang, ta có thể tự suy ra được cách tính chu vi hình thang cân, hình thang cân là dạng hình thang có 2 góc kề một đáy bằng nhau, 2 cạnh bên của hình thang bằng nhau không song song với nhau.
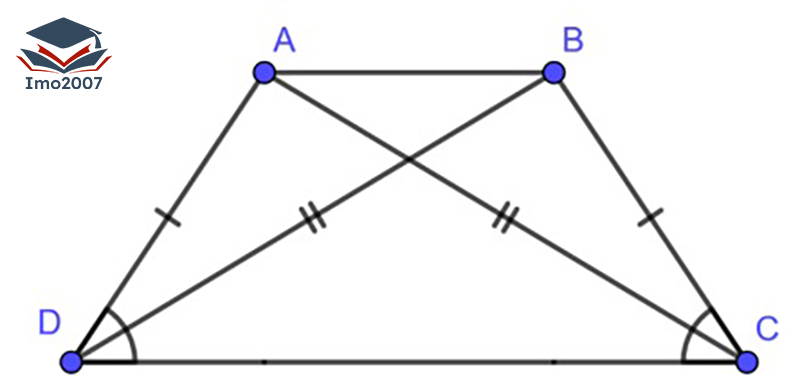
Công thức tính chu vi hình thang cân là:
Chu vi = 2a + c + d
Trong đó:
a là độ dài đáy (2 đáy đối diện bằng nhau)
c và d là độ dài 2 cạnh bên
Ví dụ, nếu ta có một hình thang cân với đáy a = 8 cm và cạnh bên cùng độ dài c = d = 5 cm, ta có thể tính chu vi như sau:
Chu vi = 2(8 cm) + 5 cm + 5 cm = 26 cm
Vậy chu vi của hình thang cân trong ví dụ trên là 26 cm.
Cách tính chu vi hình thang vuông
Hình thang vuông là hình thang có một góc vuông. Cạnh bên góc vuông là chiều cao của hình thang. Hình thang vuông có cách tính chu vi tương tự hình thang thường.
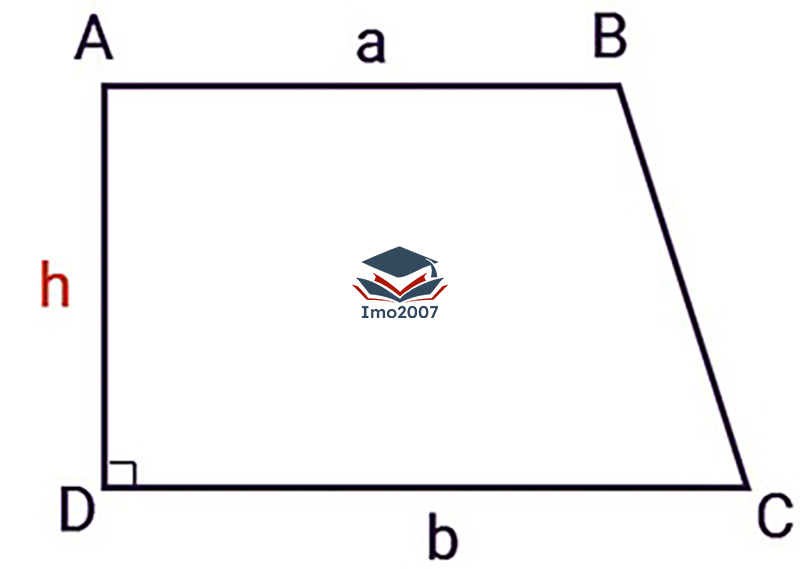
Chu vi = a + b + c + d
Ví dụ, nếu ta có một hình thang vuông với đáy lớn a = 10 cm, đáy nhỏ b = 6 cm và cạnh bên c = d = 7 cm, ta có thể tính chu vi như sau:
Chu vi = 10 cm + 6 cm + 2(7 cm) = 40 cm
Vậy chu vi của hình thang vuông trong ví dụ trên là 40 cm.
Trên đây là cách tính chu vi hình thang ở tất cả dạng hình, hi vọng các em đã có thêm những kiến thức bổ ích để nâng cao trình độ giải toán hình của mình. Imo2007 chúc các em học thật giỏi môn toán và mãi yêu thích bộ môn này.